Hydrologic and Erosion Modeling

Helena Mitasova

GIS/MEA582 Geospatial Modeling NCSU

Learning objectives

• identify geospatial modeling of landscape processes
• distinguish spatially averaged and distributed models
• compare methods for spatial hydrologic modeling
• apply modeling soil erosion, sediment transport and deposition

Geospatial modeling of processes

• Numerical simulations: tools for gaining new knowledge - virtual experiments
• Geospatial numerical simulations: the modeled quantities are function of a location on Earth

• Geospatial models have evolved:

  • from: empirical, spatially averaged, static

  • to: process-based, spatially explicit and dynamic with the aim to predict modeled quantity at any point in space and time

• Most geospatial models combine empirical and process-based approaches

Modeling components

• Modeled quantity: water depth [m], discharge [m$^3$/s], pollutant concentration[mg/l]
• Spatial and temporal scale: e.g. modeling a first order stream may require 1m spatial and 1 min temporal resolution
• Configuration space and interactions: water depth depends on precipitation, topography, soils, land use
• Governing equations: continuity equations, diffusion, ...

Geospatial representation

• Modeled quantities and environmental variables can be represented by continuous georeferenced fields
• To support numerical simulations these fields need to be discretized:
  • spatially averaged units: discrete polygons (hydrologic units, hillslope elements, landscape patches)
  • spatially distributed representation: structured and unstructured meshesi (grids), or random particles
  • modeled quantities can also evolve along networks (streams, sewer networks) or represent discrete objects (particles, agents)

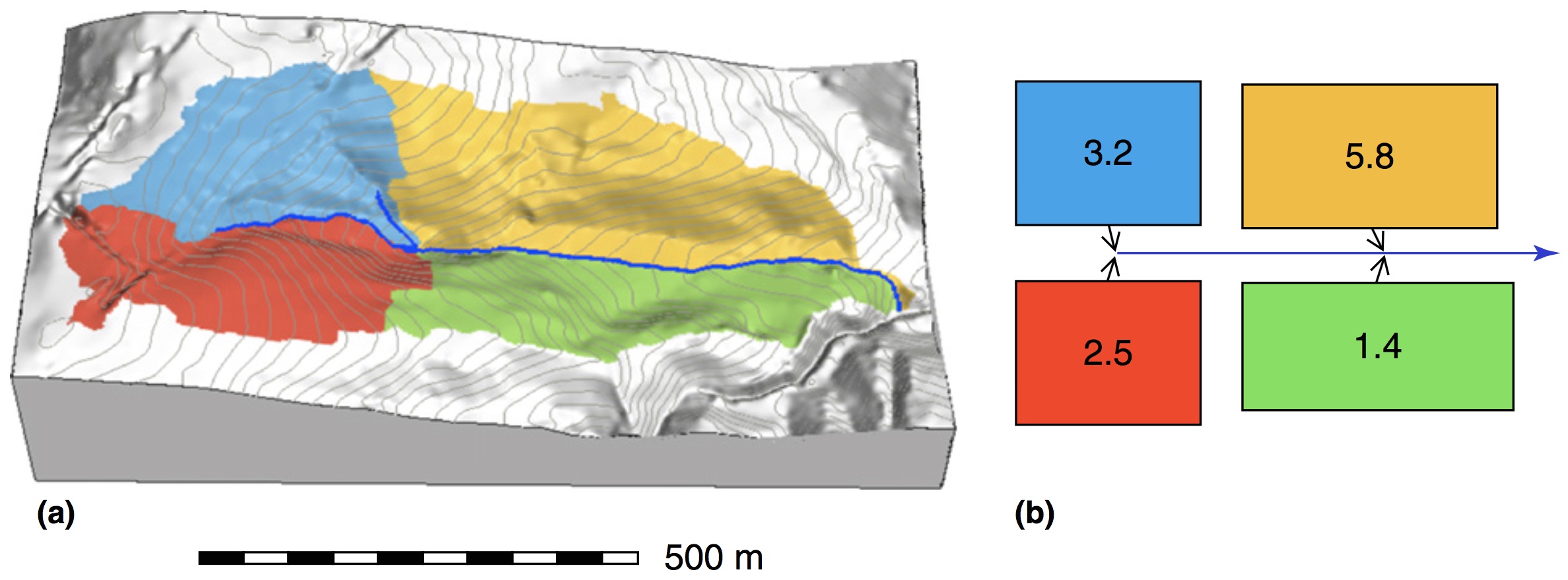
Spatially averaged models

• Spatially averaged models predict the modeled variable for each averaged unit, such as watershed, the result is discrete polygons or a number

Spatially distributed models

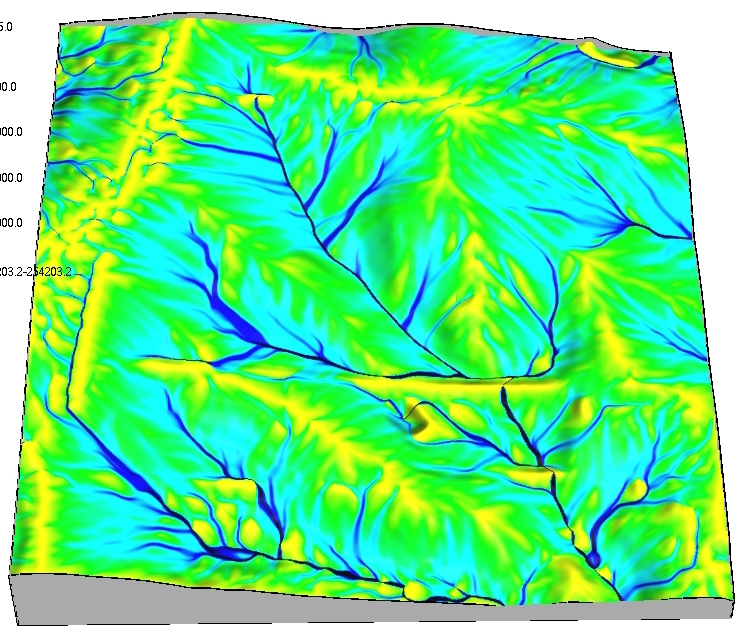
• Spatially distributed or spatially explicit models predict the variable at any point in space and the result is continuous field

Geospatial modeling and GIS

• workflow using standard GIS tools: simple empirical models with physics based components
• models fully integrated as modules: complex physics-based or empirical models
• models linked to GIS as extensions or add-ons: common structure and interface
• complex modeling systems linked through data: GIS is used for input data processing, results analysis and visualization, but the model is independent from GIS.
• complex modeling systems can incorporate selected GIS capabilities

Hydrologic modeling

surface water flow

Empirical model: Rational equation

• Simplest approximation of discharge from small watersheds
• Assumes steady state, uniform rainfall excess and constant velocity
• Discharge is then sum of rainfall excess produced by each grid cell routed to the outlet

Rational equation

$$ Q = C \, i \, A $$

• $Q$ [$\rm m^3/s$] is maximum rate of runoff (discharge)

• $C$ is runoff coefficient (ratio of rainfall that becomes runoff : forest 0.05-0.25, pavement 0.75-0.95)

• $i$ [$\rm m/s$] average rainfall intensity

• $A$ [$\rm m^2$] is upslope contributing area

• to determine $i$ we need time to concentration (time water needs to flow along the longest flowpath to reach the outlet), duration of rainfall needed to reach the steady state

Rational equation

$$ Q = C \, i \, A $$

Spatially Distributed Models

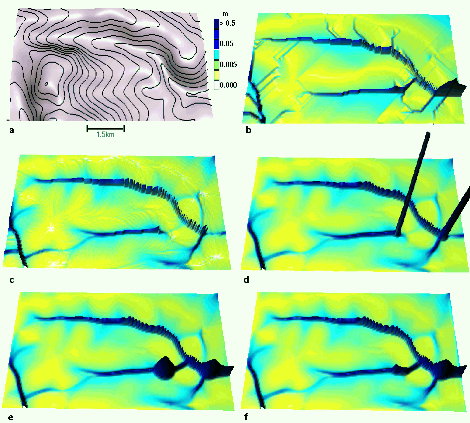
Dynamic Hydrologic Models

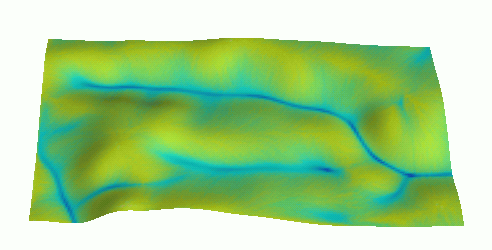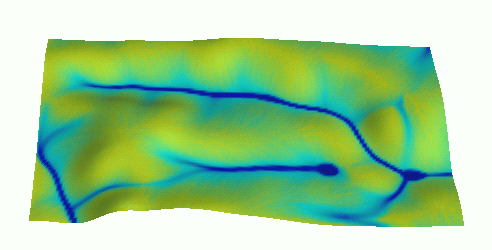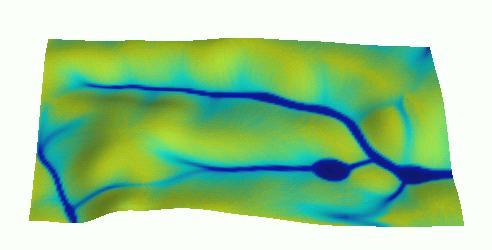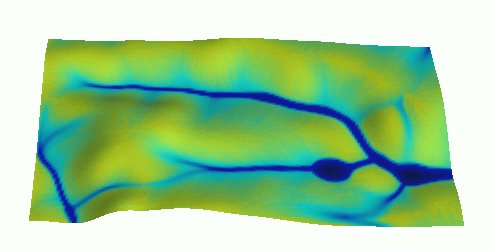
Instead of filling the DEM, we fill the depression with water

Path sampling method

• duality between particle and field representation
• path sampling: water evolving according to the shallow water bivariate continuity equation - drift and diffusion

Overland water flow

Path sampling based simulation of water flow within a small agricultural watershed

Note simulation of ponding and dispersed flow over the road

Water flow in a suburb

High resolution (sub-meter) modeling of runoff

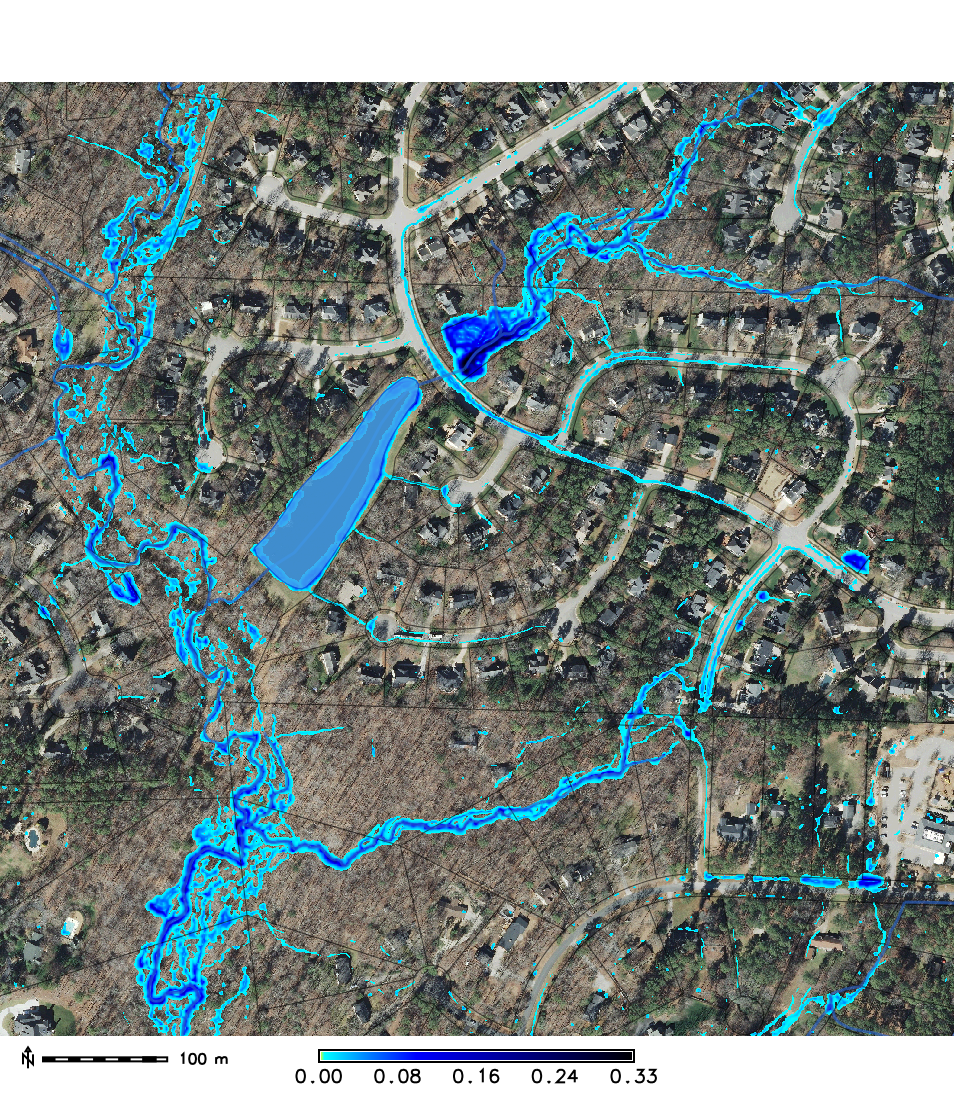
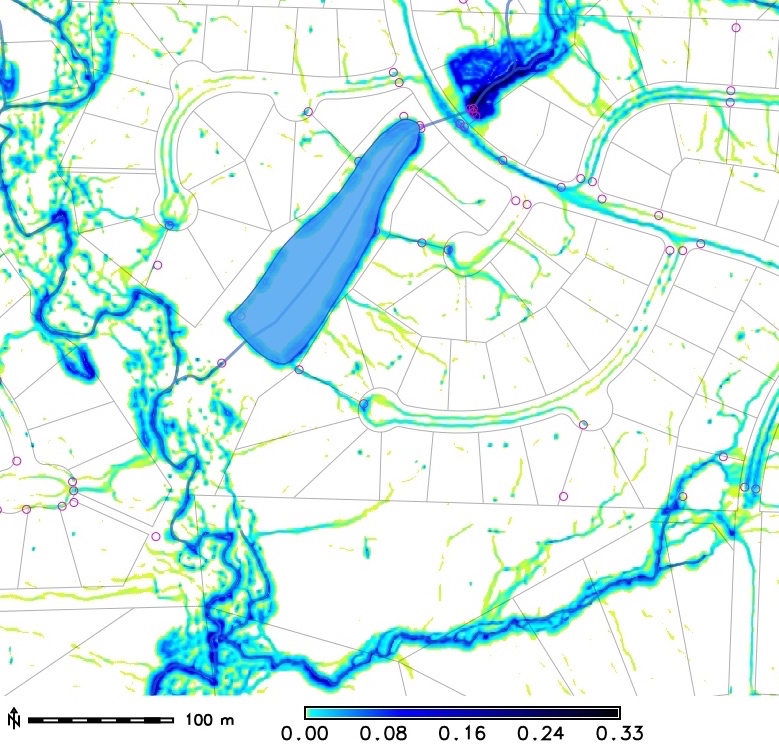
Note (a) the role of stream buffer in storing water and slowing down the flow, (b) accurate routing of water on roads along curbs indicating high accuracy of the lidar-based DEM

Soil erosion modeling

• Modeled quantity: sediment transport rate [kg/(ms)], net erosion/deposition rate [kg/(m$^2$s)]
• Spatial and temporal scale: from hillslopes to watersheds, minutes (storms), annual rates
• Configuration space and interactions: sediment transport depends on water flow, topography, soil properties, land use
• Governing equations: continuity equation, diffusion, proliferation and decay

Sediment transport equations

Assuming steady state flow, sediment transport by shallow water flow $q_s$ [kg/(ms)] can be approximated by sediment transport capacity $T_c$:

$$ q_s \approx T_c = K_T A^m (\sin \gamma)^n$$

• where $A$ is contributing area as measure of water flow
• $K_T$ is transport capacity coefficient
• $\gamma$ is slope angle
• $m,n$ are empirical coefficients, control the relative influence of flow accumulation and slope

Evolution of sediment transport

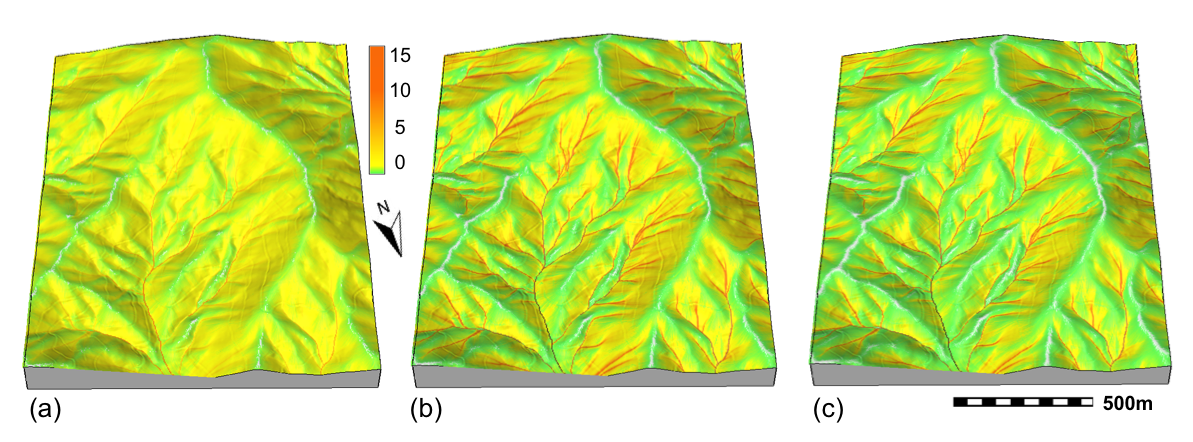
Sediment transport capacity regimes

Net erosion and deposition

Net erosion and deposition rate = change in sediment transport capacity $T_c$ in the direction of flow $\alpha$ = divergence of the sediment transport vector field:

$$d_s =\nabla\cdot {\bf q}_s \approx {\partial (T_c \cos \alpha ) \over {\partial x}} + {\partial (T_c \sin \alpha ) \over {\partial y}}$$

Equation is easy to compute using functions for partial derivatives and map algebra. Note that partial derivatives of a surface can also be computed using its slope $\beta$ and aspect $\alpha$ and keep in mind that instead of elevation our surface is the sediment transport capacity field:

$$ {{\partial z} \over {\partial x}} = \tan \beta \cos \alpha $$ $$ {{\partial z} \over {\partial y}} = \tan \beta \sin \alpha $$

Net erosion and deposition

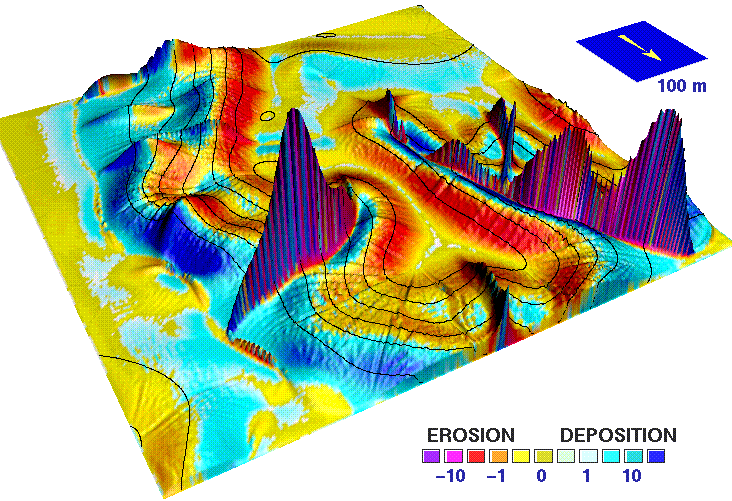
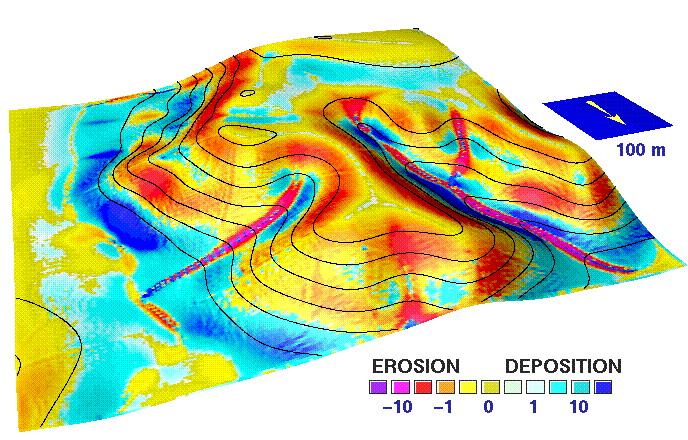
Net erosion and deposition draped over sediment transport capacity surface (left) and draped over elevation surface (right)

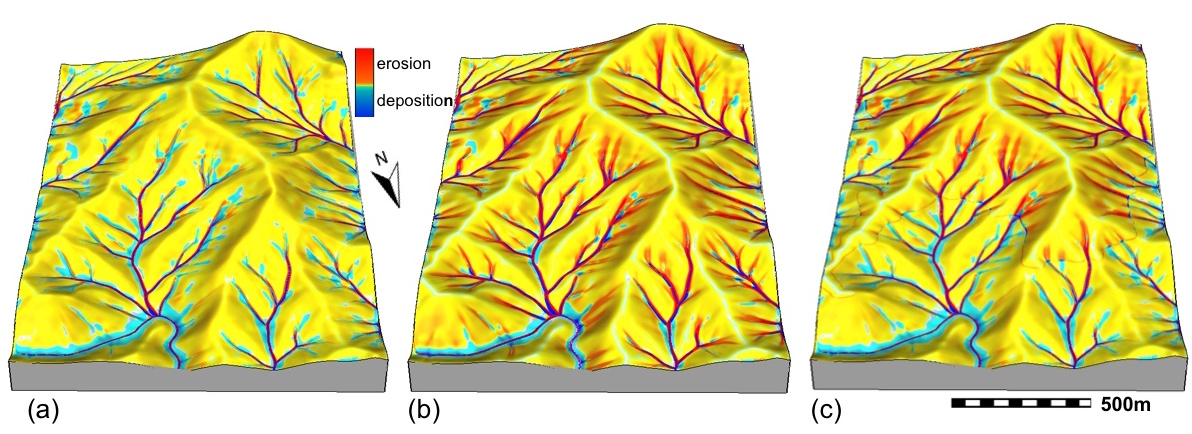
Net erosion-deposition regimes

Empirical equations

• R - rainfall erosivity factor
• K - soil erodibility factor
• L - hillslope length or contributing area
• S - slope steepness factor
• C - cover-management factor
• P - protection measures factor

$L$ is a function of water flow over tilted plane, for complex topography we can replace it by $A$, upslope contributing area and modify RUSLE to estimate sediment transport capacity and net erosion-deposition as a change in sediment transport in the direction of flow.

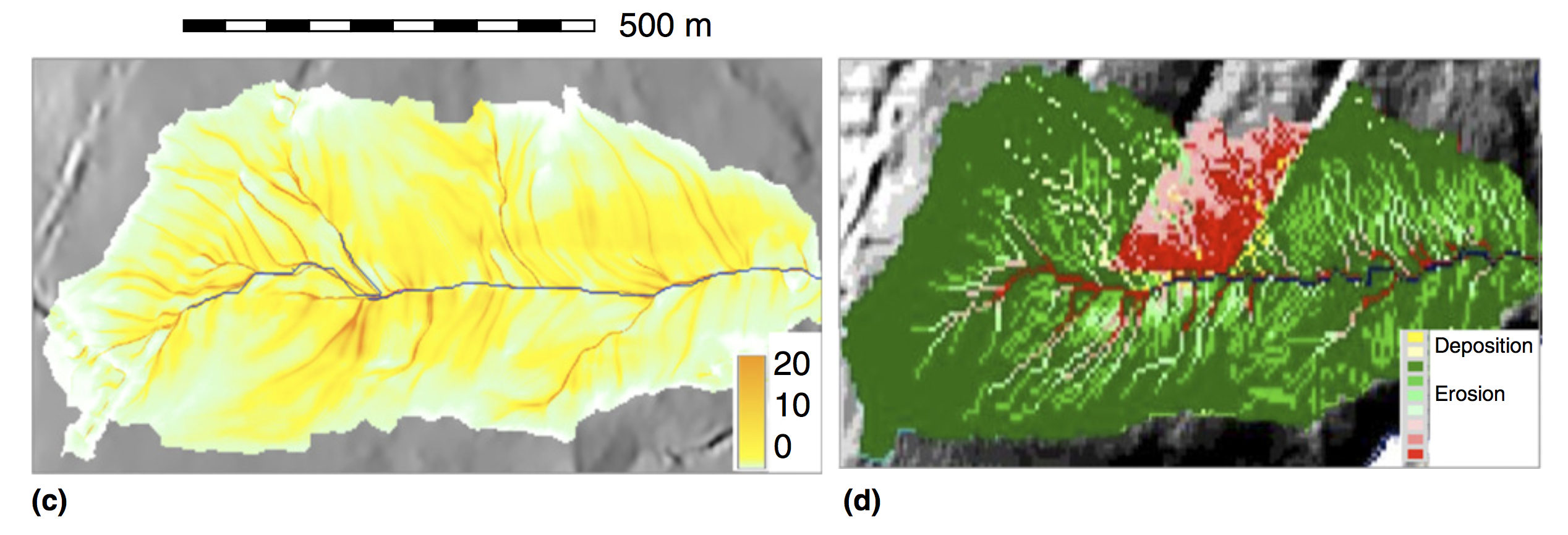
Sediment transport capacity

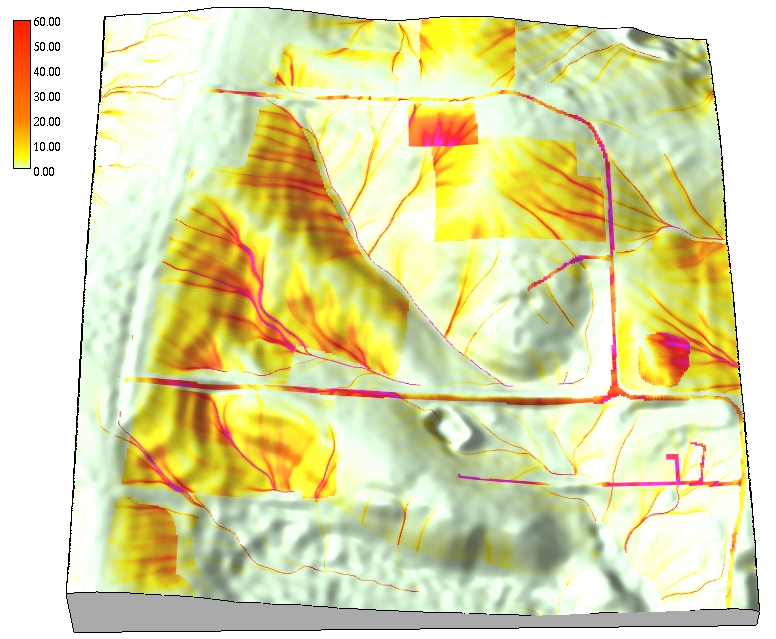
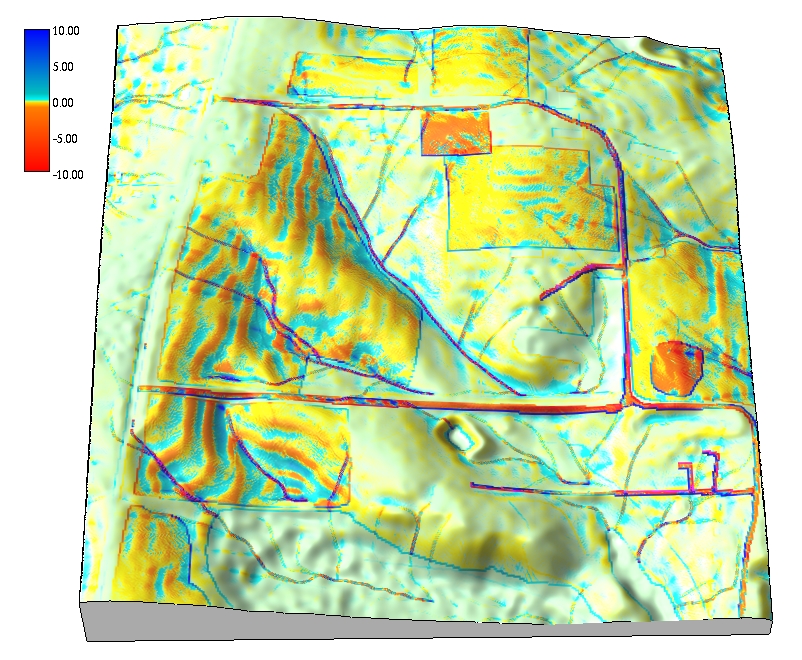
Net erosion and deposition

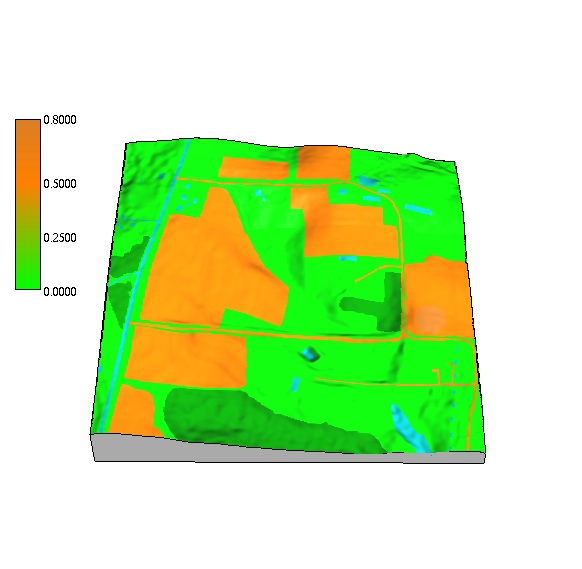
Read Brief theoretical background document for detailed description of the equations and units used in the assignment

Land use change application

Impact of construction on overald flow and erosion

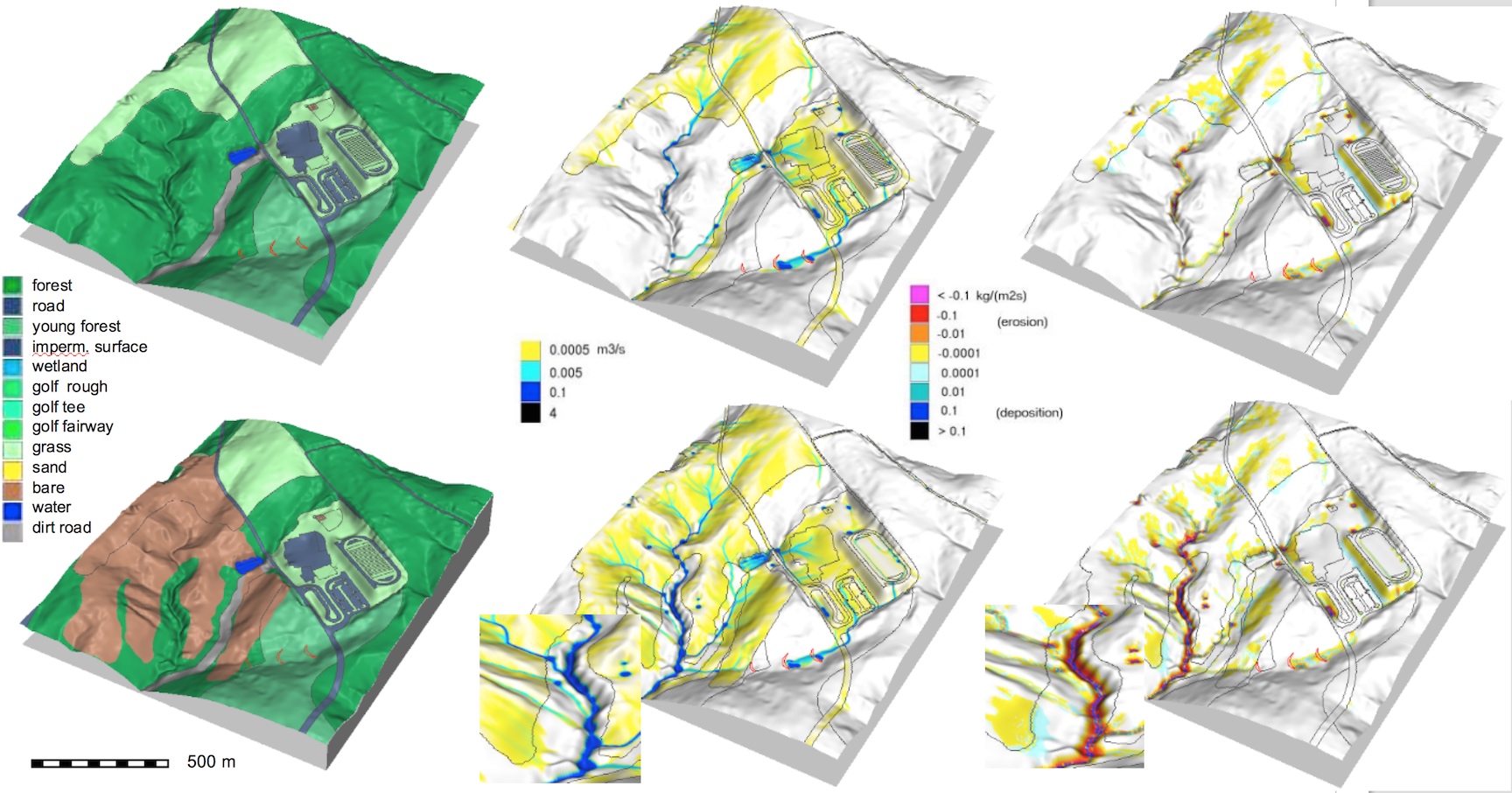
Note the highest erosion rates along the stream banks

Summary

• we defined spatially averaged and distributed models and explained linking GIS and landscape process modeling
• we compared methods for spatial hydrologic modeling from simple empirical equation to process-based models
• we explained modeling soil erosion, sediment transport and deposition using empirical and processed based models
• we learned about applications of flow modeling using high resolution, lidar-based DEMs