Spatial Interpolation: Splines
Helena Mitasova
GIS/MEA582 Geospatial Modeling and Analysis NCSU
Outline (learning objectives)
- Spline interpolation
- Spline parameters: tension and smoothing
- Evaluating interpolation accuracy: deviations, crossvalidation
- Special cases: contours, anisotropy
- Processing large point data sets: segmentation, subsampling
- Multivariate interpolation: volumes, topo-climatology, dynamic volumes
Interpolation with radial basis functions (RBF)
- Variational approach is based on minimizing:
- deviations from the given points
- smoothness seminorm or roughness penalty
- Radial basis functions: multiquadrics, splines
- Physics-based interpretation: spline function is a thin flexible plate with tunable bending energy
- Formally equivalent to universal kriging
Splines: general equation
$$ F(r) = T(r) + ∑ λ_j R(r,r_j) \; j=1,m $$
- $r = (x,y)$ is location of a grid point,
- $r_j=(x_j,y_j$) is location of a measured point
- $λ_j$ are coefficients
- $R(r,r_j)$ is a radial basis function
- $T(r)$ is a trend:
low order polynomial: $a_0$, $a_0+a_1x+a_2y$, ...,
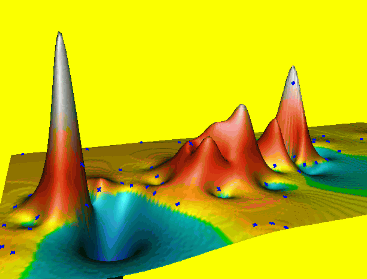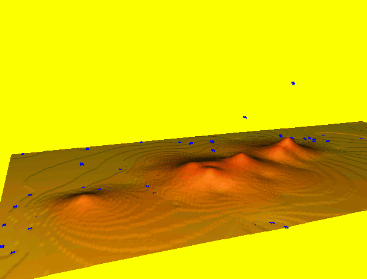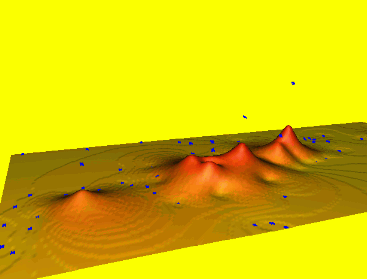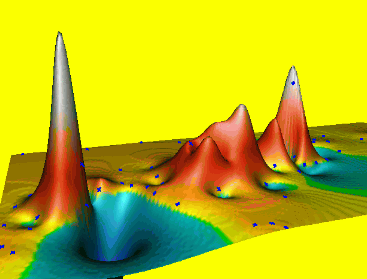
Splines with different properties
Spline properties depend on the formulation of smoothness seminorm or roughness penalty
- thin plate spline ($2^{nd}$ order derivatives)
- spline with tension ($1^{st}$ and $2^{nd}$ order derivatives)
- regularized spline ($2^{nd}$ and higher order)
- regularized spline with tension (derivatives of all orders with decreasing weight)
- see the smoothness seminorms in Table 1
- see example equations for $R(.)$ here
Note: Functions with $2^{nd}$ order derivatives minimize curvatures
Regularized spline with tension (RST)
$$ F(r) = T(r) + ∑ λ_j R(\varphi |r-r_j|) \; j=1,m $$
- $\varphi$ is the tension parameter and
- $|r-r_j|$ is the squared distance between the unsampled and measured points.
- minimizes seminorm with all derivatives with decreasing weight
Spline tension rescales distances, it has similar effect to adjusting the range in kriging or the distance weight exponent in IDW
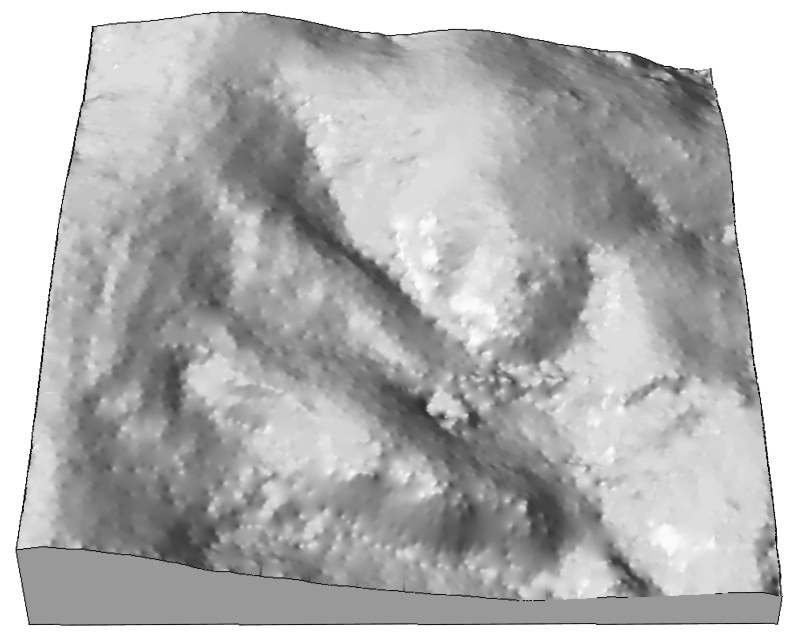
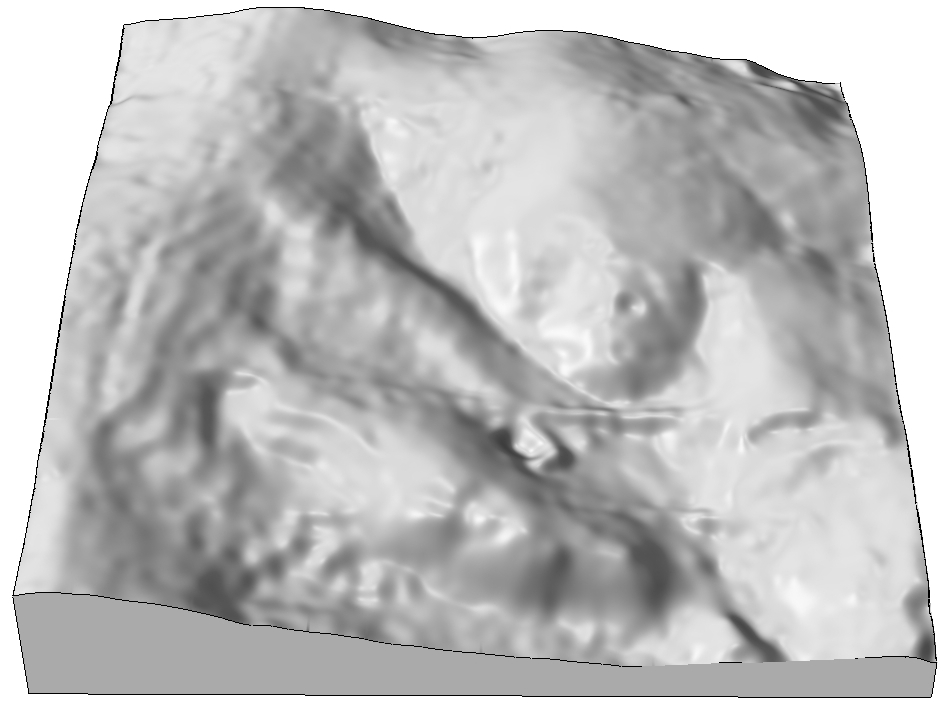
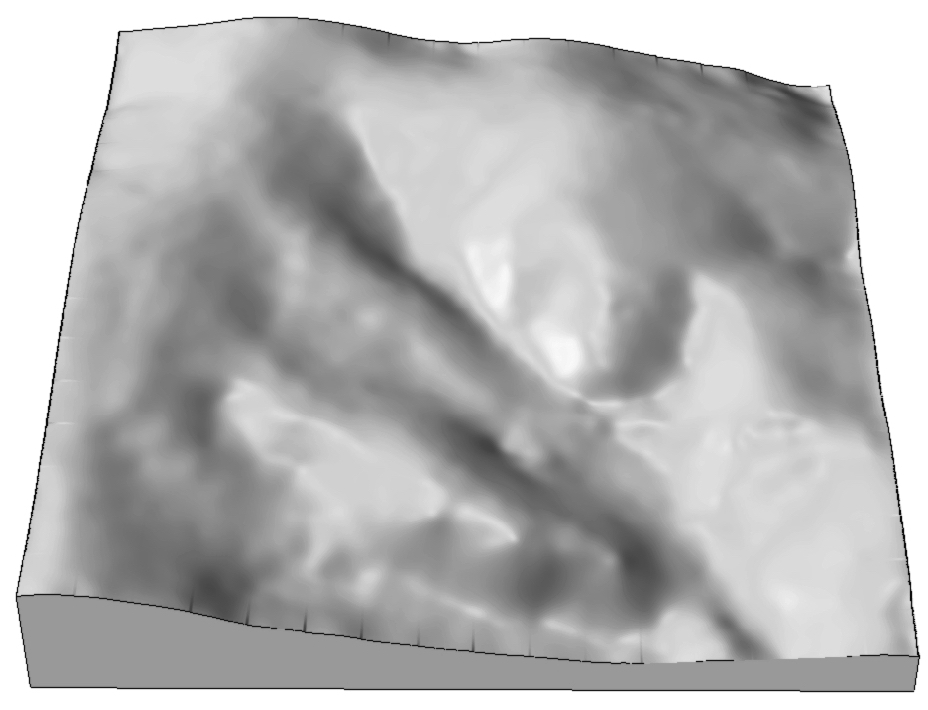
Spline: tension parameter
Tension controls the stiffness of the plate:- high tension: soft rubber sheet, short range
- low tension: stiff steel plate, long range
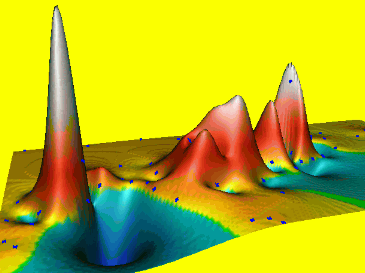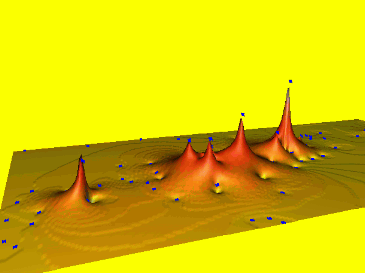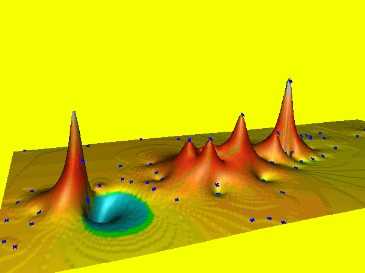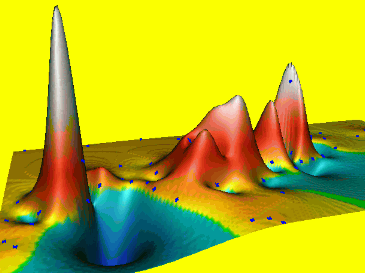
Spline: tension parameter
Spline: smoothing parameter
Allows the surface to deviate from measured points
$$F(x_i,y_i) = z(x_i, y_i) + \varepsilon(x_i,y_i)$$
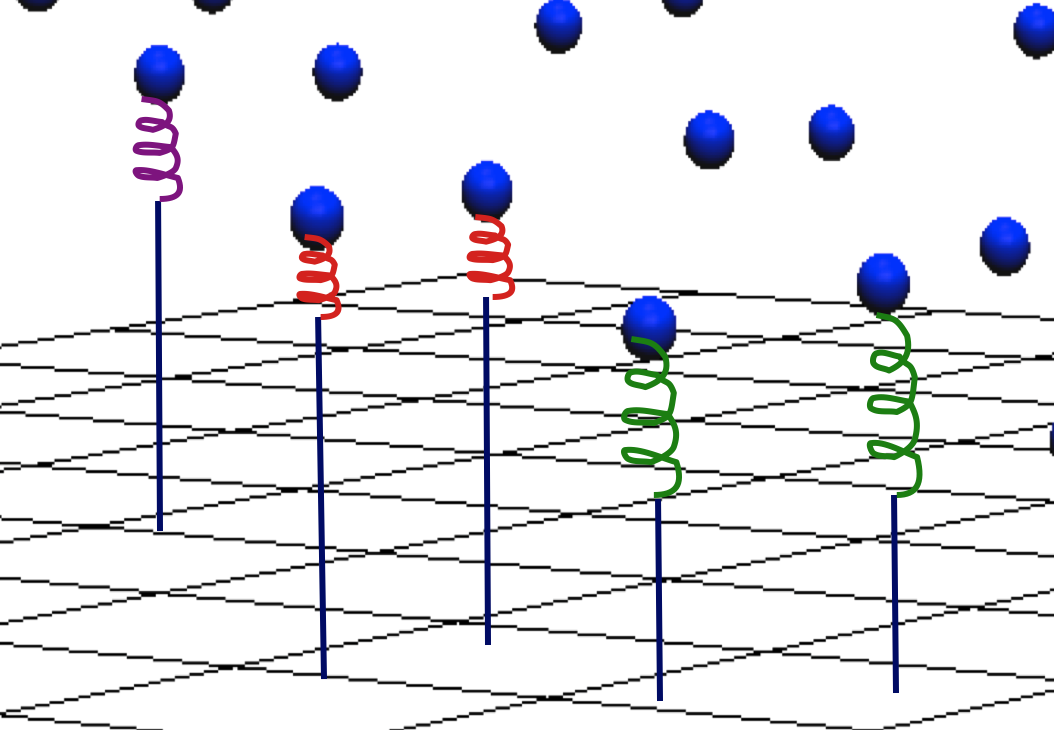
Reduces overshoots, smoothes out noise, improves numerical stability. It can be applied to individual points.
Spline: smoothing
Smoothing controls the deviation from the data points, large smoothing results in trend surface $T(x,y)$

Smoothing spline applied to concentrations of COVID-19 virus in wastewater
Spline: smoothing
Smoothing can be spatially variable

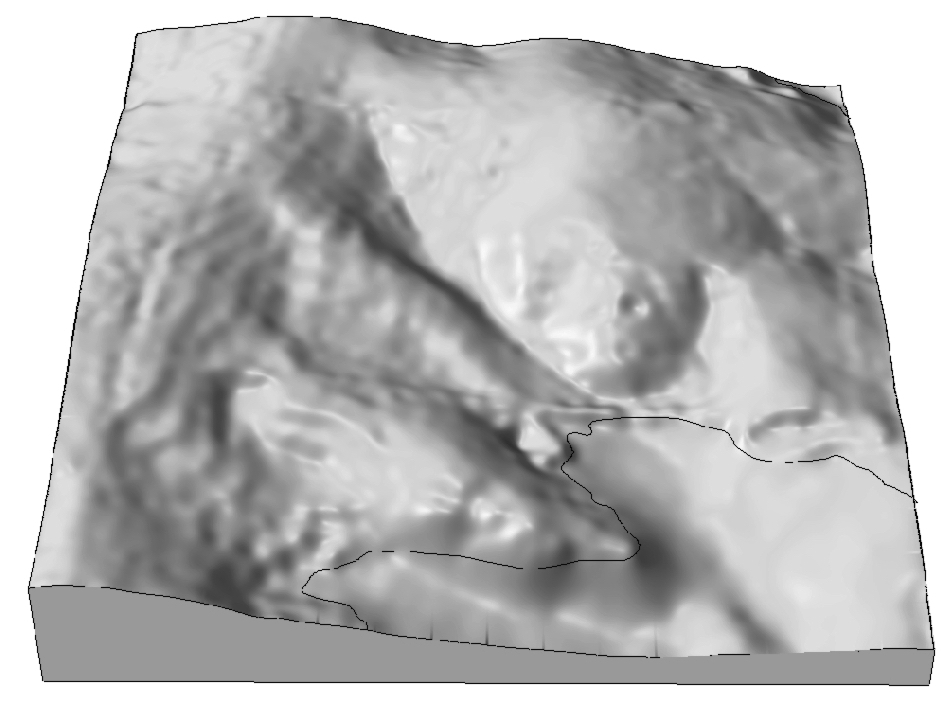
Spline implementations
- Spline with tension: numerical solution supports carved streams, but here the tension is too high
- Explicit RST method: lower tension combined with smoothing reduce bias towards given points
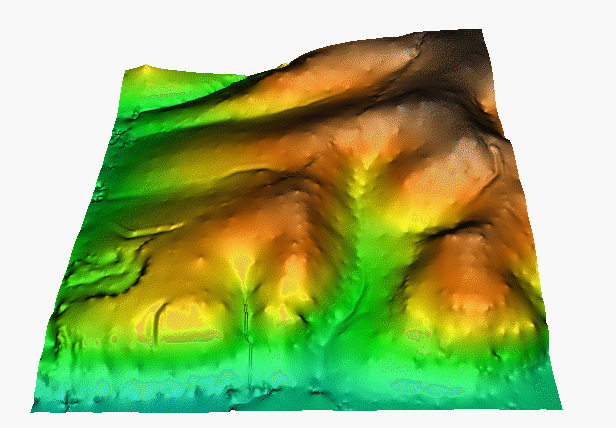
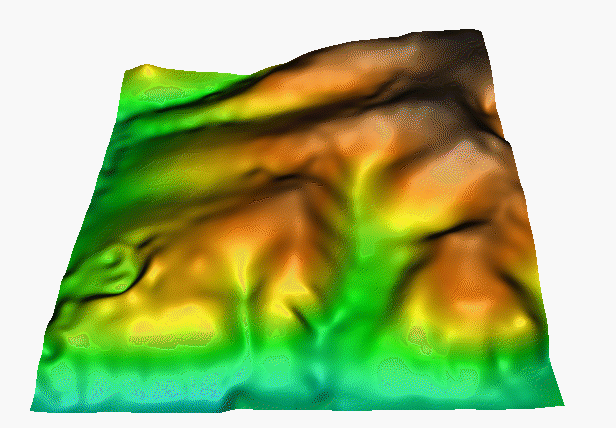
Interpolation with anisotropy
Anisotropic tension: rescaling distances in a given direction changes the range of influence in this direction, leading to anisotropic pattern in the resulting surface
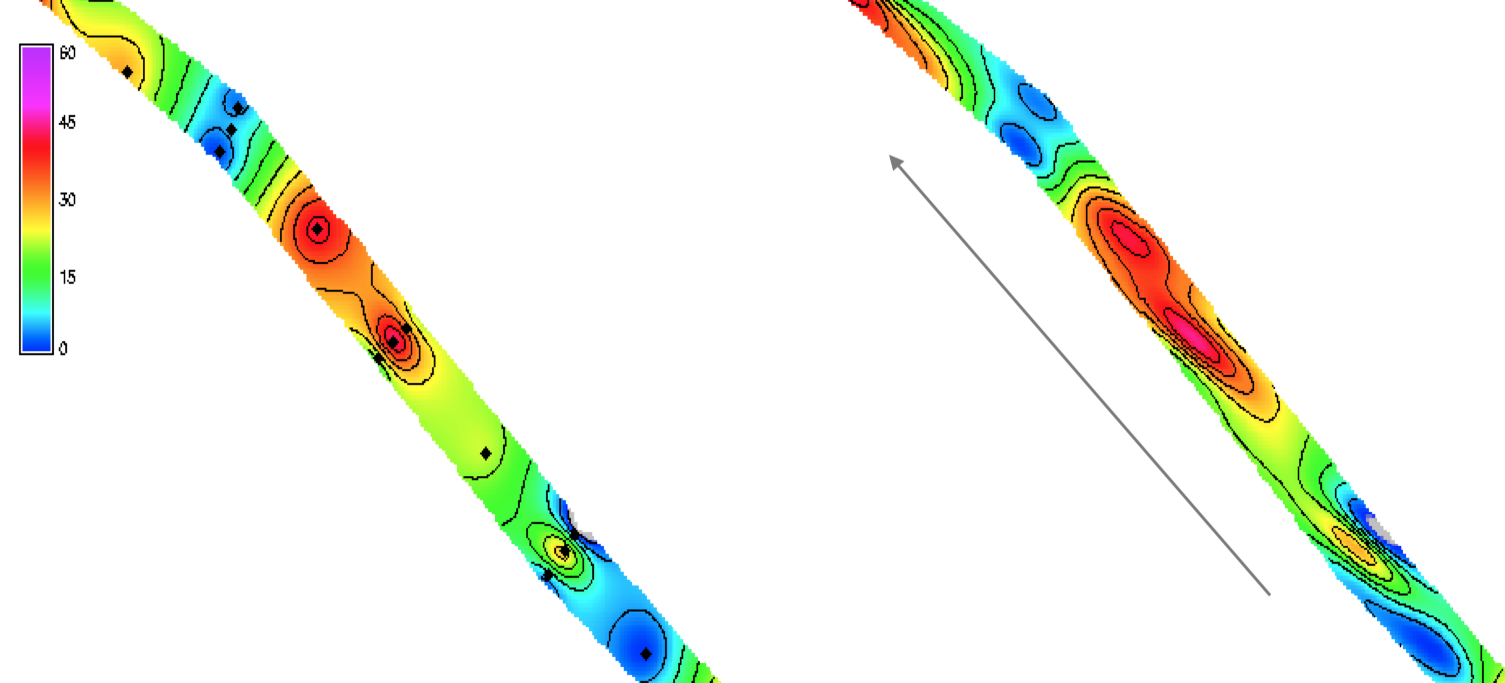
Data from Genereux, D.P., S. Leahy, H. Mitasova, C.D. Kennedy, and D.R. Corbett, 2008, Spatial and temporal variability of streambed hydraulic conductivity in West Bear Creek, NC, J. Hydrology, 358, p. 332-352
Interpolation from profiles
- GPS-based sensors: dense sampling along a line
- use anisotropy to rescale distances between profiles, minimize artifacts
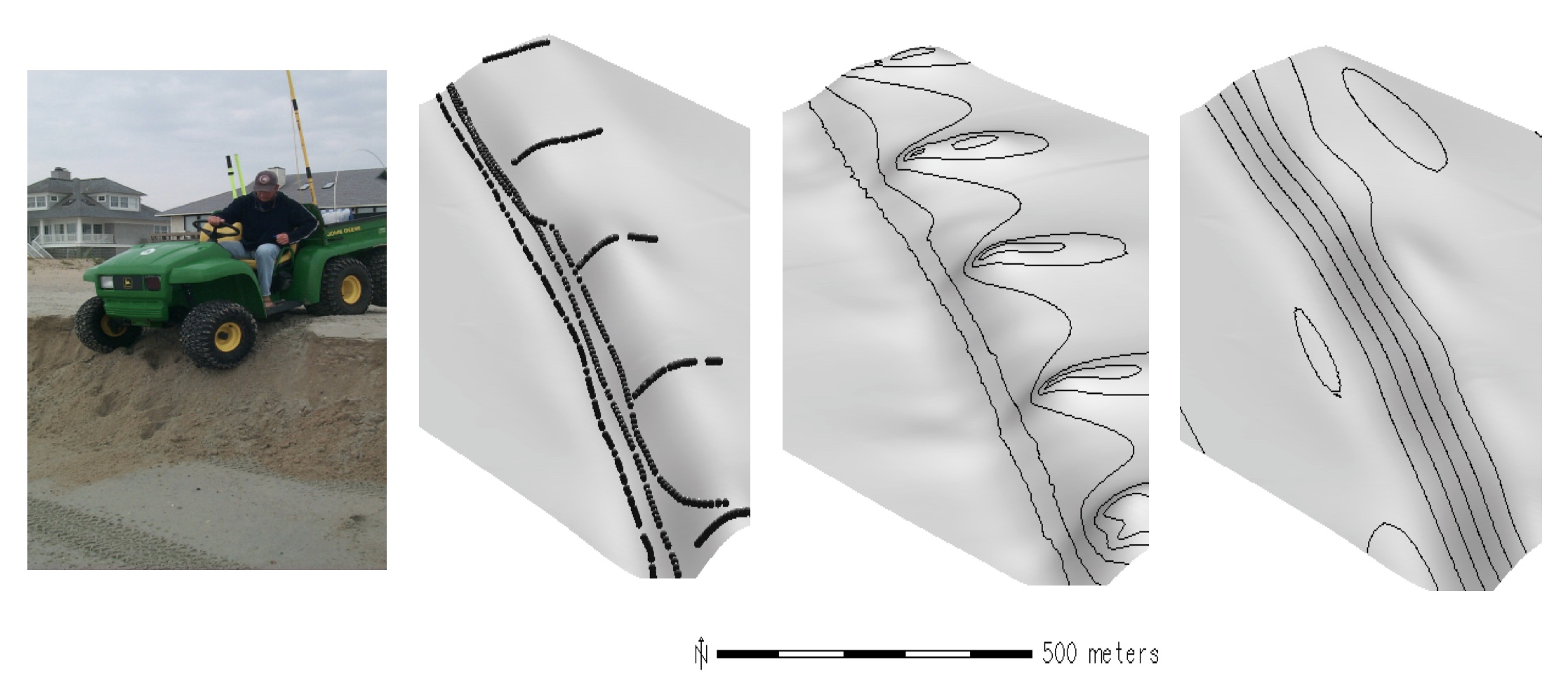
Better alternative is to map the beach with a drone using structure from motion
Interpolation accuracy
- Effect of smoothing: deviations from given points
$$ dz (x,y) = z' (x,y) – z (x,y) $$
where $z'$ is the interpolated value and $z$ is the given value
- Predictive accuracy: crossvalidation error
$$e_z (x,y) = z' (x,y) – z_o (x,y)$$
where $z'$ is the interpolated and $z_o$ is the given value in a point that was omitted from the set of points used for the interpolation. n-interpolations are performed, each time omitting one point in which $e_z$ is computed: also called leave-one-out cross-validation (LOOCV)
- Artifacts, bias can be found using histograms, aspect maps, curvatures
Interpolated surface deviations
Deviations map for smoothing 0.1 and 10
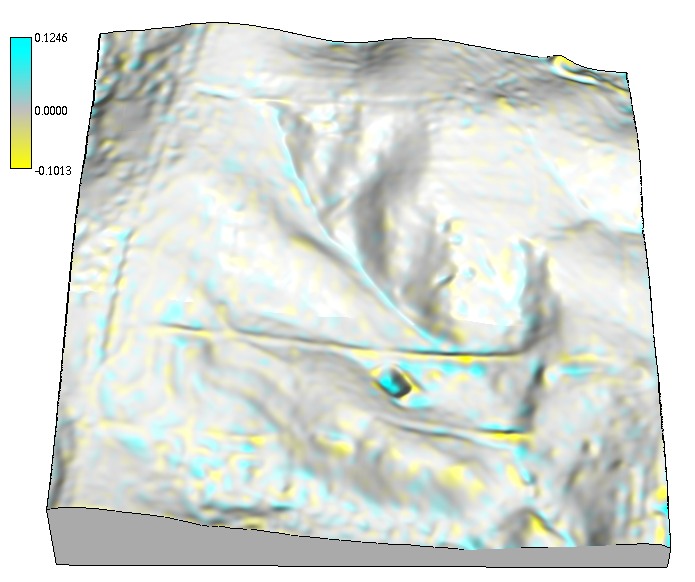
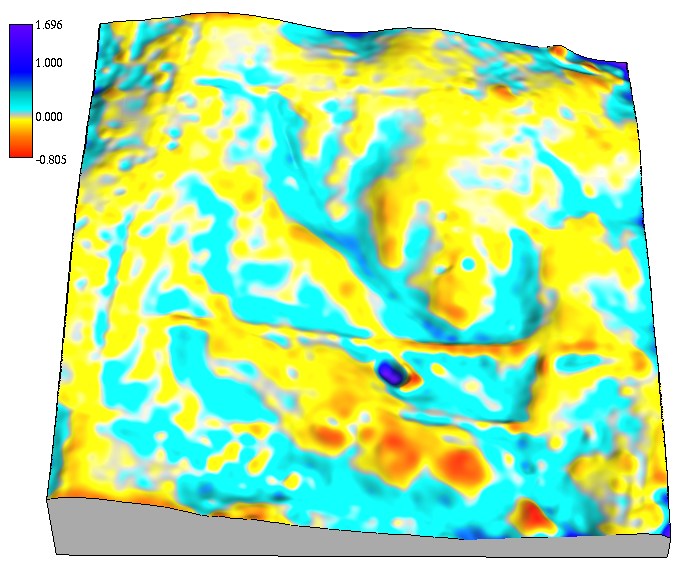
Color maps of differences between the given and interpolated values draped over the DEMs
Interpolated surface predictive errors
Map showing spatial pattern of predictive errors

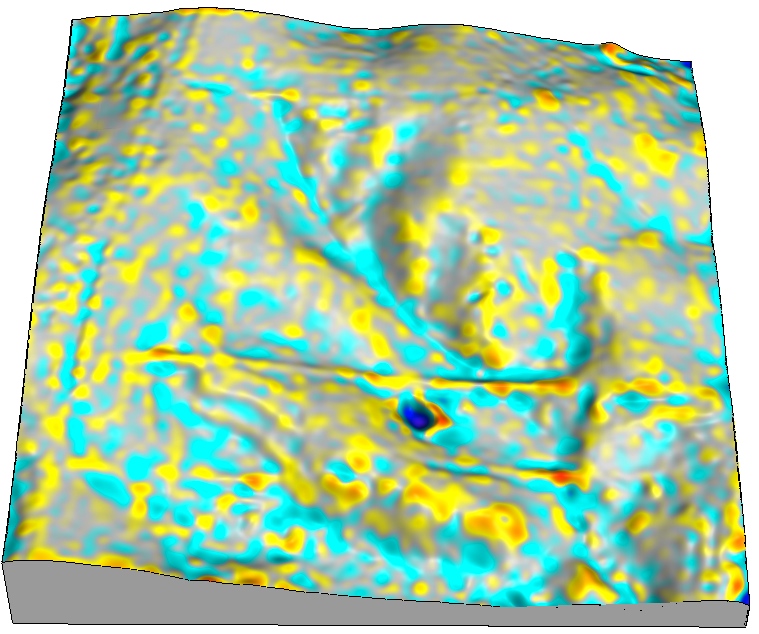
Map of differences between the interpolated and given values in a point that was omitted from the set of points used for the interpolation (leave one out cross-validation), shown with given set of points and draped over DEM.
Solutions for large data sets
- Measured point data often include thousands to millions of points (point clouds)
- To compute the coefficients of interpolation function we need to solve a system of $n$ linear equations, where $n$ is number of given points.
- To keep $n$ small we compute interpolation locally with optimized search or apply segmented processing
Segmented processing
- Segmented processing splits the region into rectagular segments
- each rectangular segment has approximately same number of measured points
- interpolation is performed for all grid points within the segment
- interpolation function is computed using measured points within the segment and its neighborhood
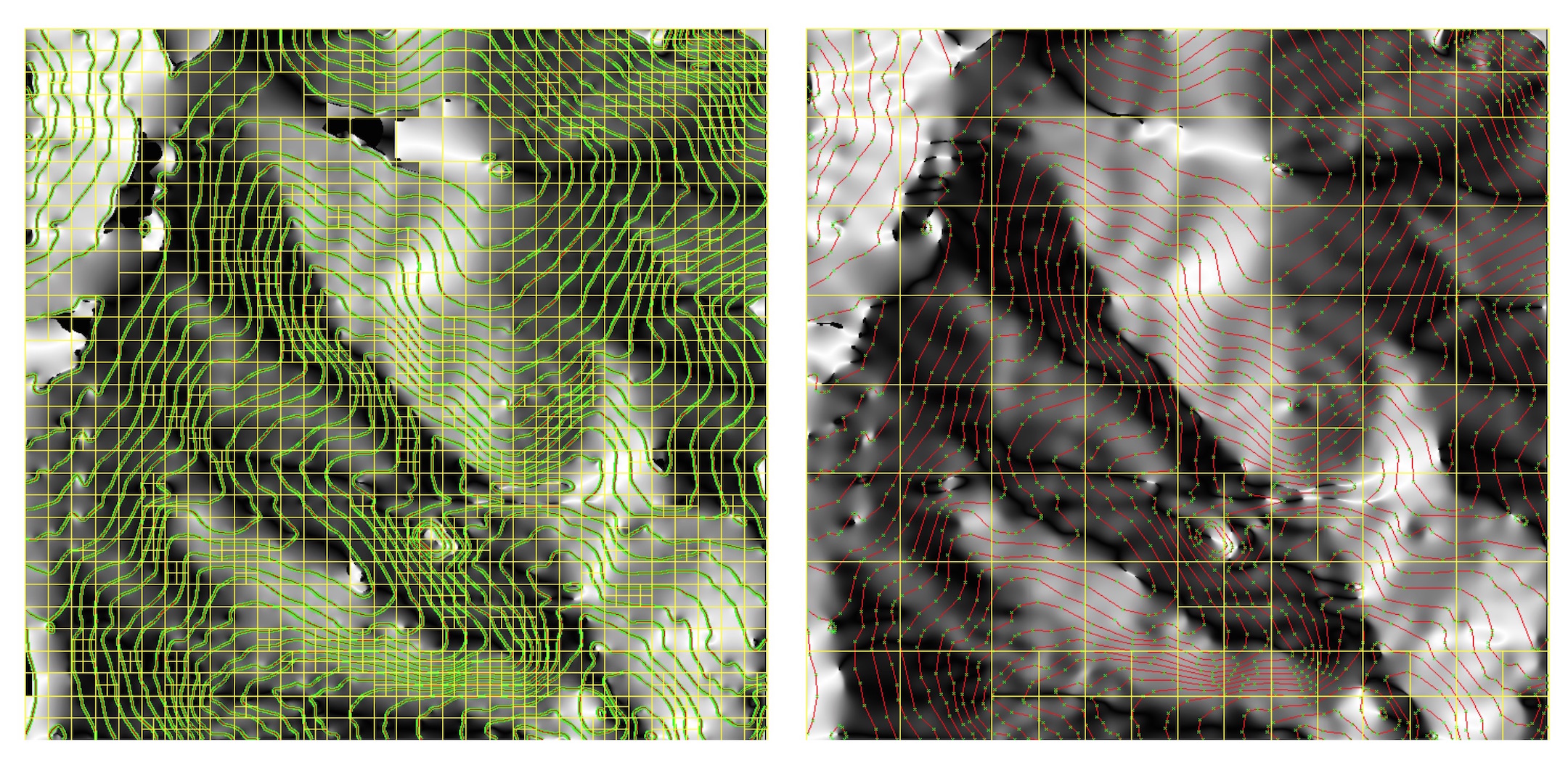
Quadtree segmentation
- if the number of points within a rectangle is larger than given maximum, it is split into 4 smaller rectangles.
- dynamic search window is used to find overlapping points to ensure smooth connection of segments
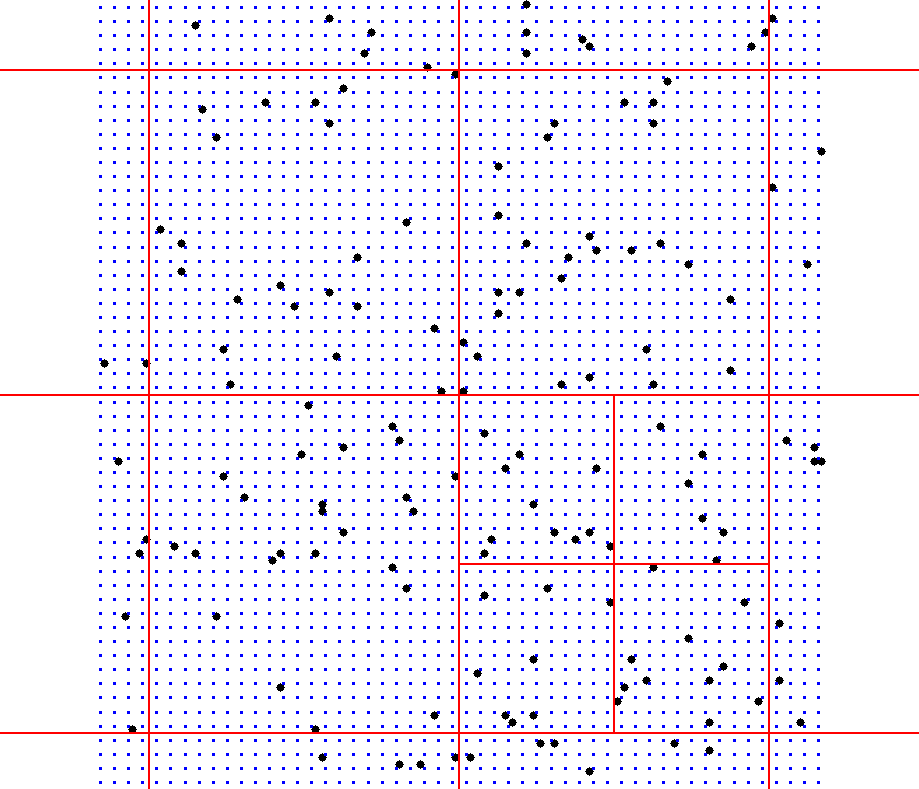
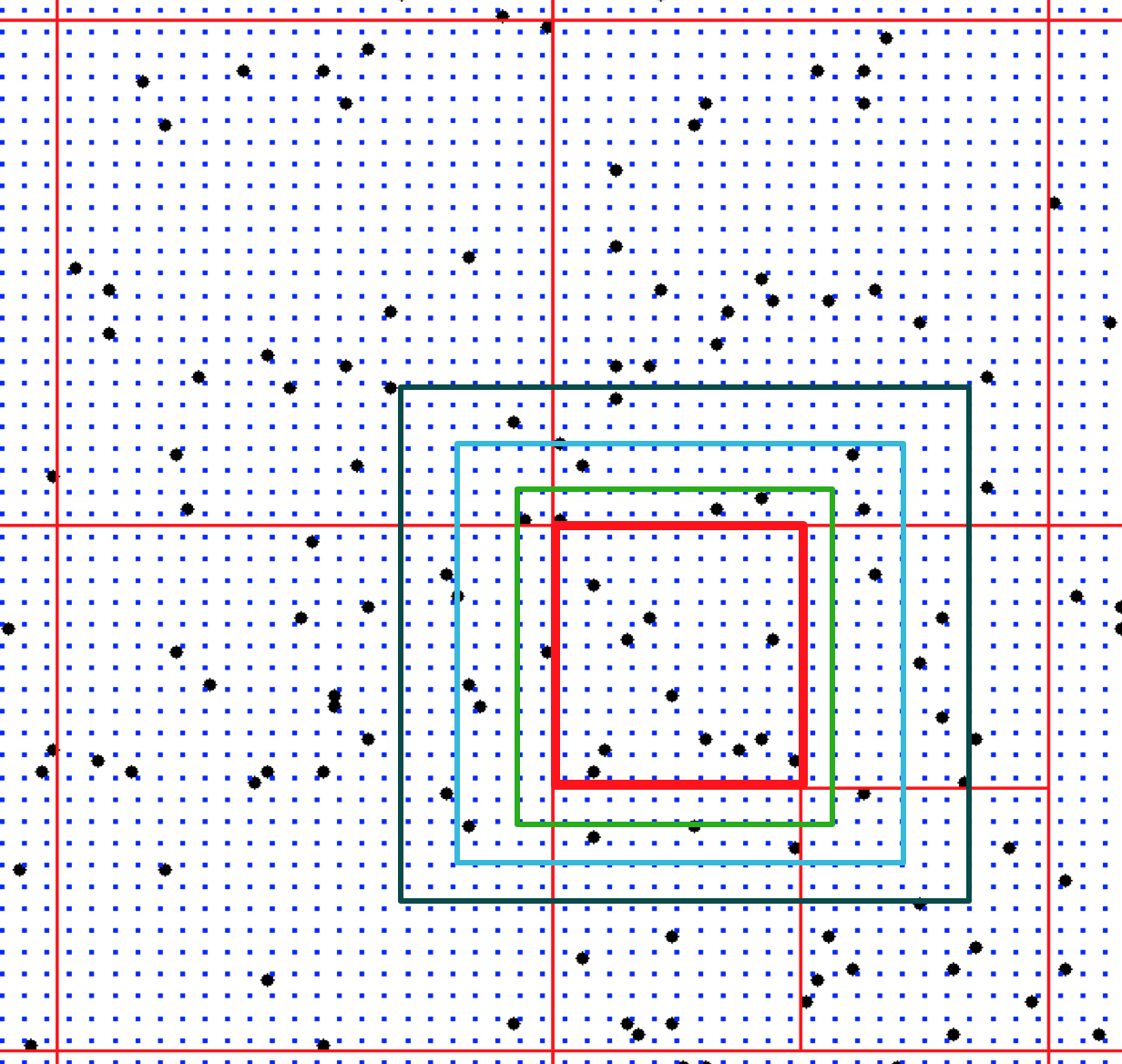
Quadtree segmentation
Interpolation of a river bathymetry using quadtree segmentation
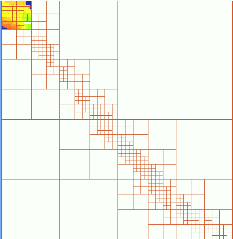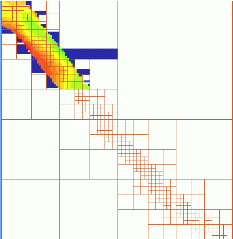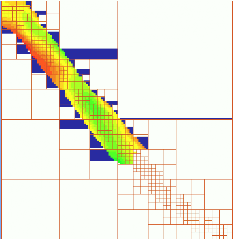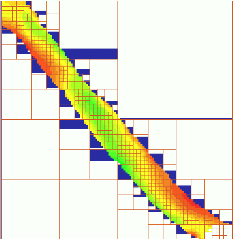
Oversampling in point measurements
Automated point data acquisition often leads to large data sets with redundant points. Examples:- point clouds acquired by lidar
- point data along profile collected automatically by GPS
- scanned contours converted to points

Point density reduction
- Can we interpolate a 2D grid if we have points with identical $x,y$ but different $z$?
- How do we define identical?
- minimum distance at which two points are considered two independent measurements (usually horizontal accuracy of the measured data)
We can eliminate points where $d_{i,j} > d_{min}$, usually $d_{min}$ is a function of data accuracy and grid resolution, often leading to much faster computation while preserving the level of detail.
Optimized subsampling
If the density of points along contours is high, spline with high tension leads to steps along contours. Solution:- Subsample points based on distance and shape.
- Example: reduction from 40,000 to 3000 points - no visible change in isoline geometry
Interpolation with optimized subsampling
Point reduction and lower tension improves the result, while computation is 10-times faster with no artifacts
Subsampling lidar point clouds: 50-90% points can be often removed leading to much faster interpolation and fewer artifacts
Multivariate spline interpolation
- Given $m$ points measured in 3D space, find such trivariate spline function $F(x,y,z$) that for each $i=1,m$ $$ w_i=F(x_i,y_i,z_i) $$
- and compute $w_k=F(x_k,y_k,z_k)$ in 3D grid points
- Similarly for points measured in 4D space (3D + time): $w_i=F(x_i,y_i,z_i,t_i)$
- we use the quadvariate spline to compute a 4D grid (or a series of 3D grids)
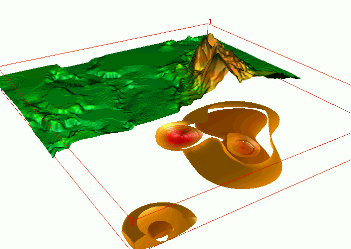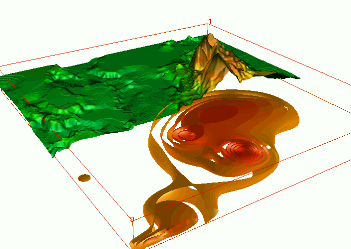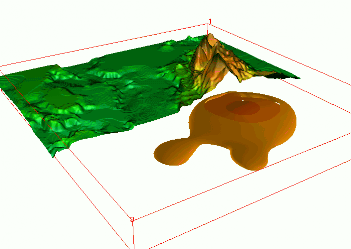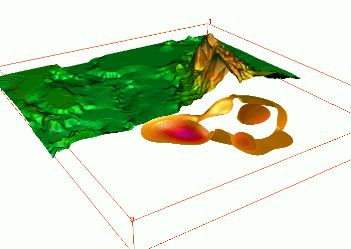
Trivariate Interpolation: volume
Nitrogen concentrations $w_i$ in the Chesapeake Bay sampled at points $(x_i,y_i,z_i)$ with different depths
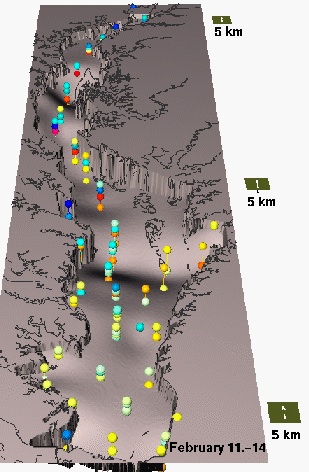
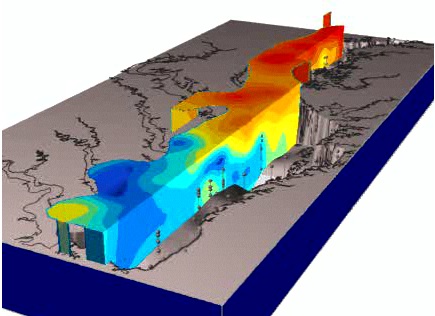
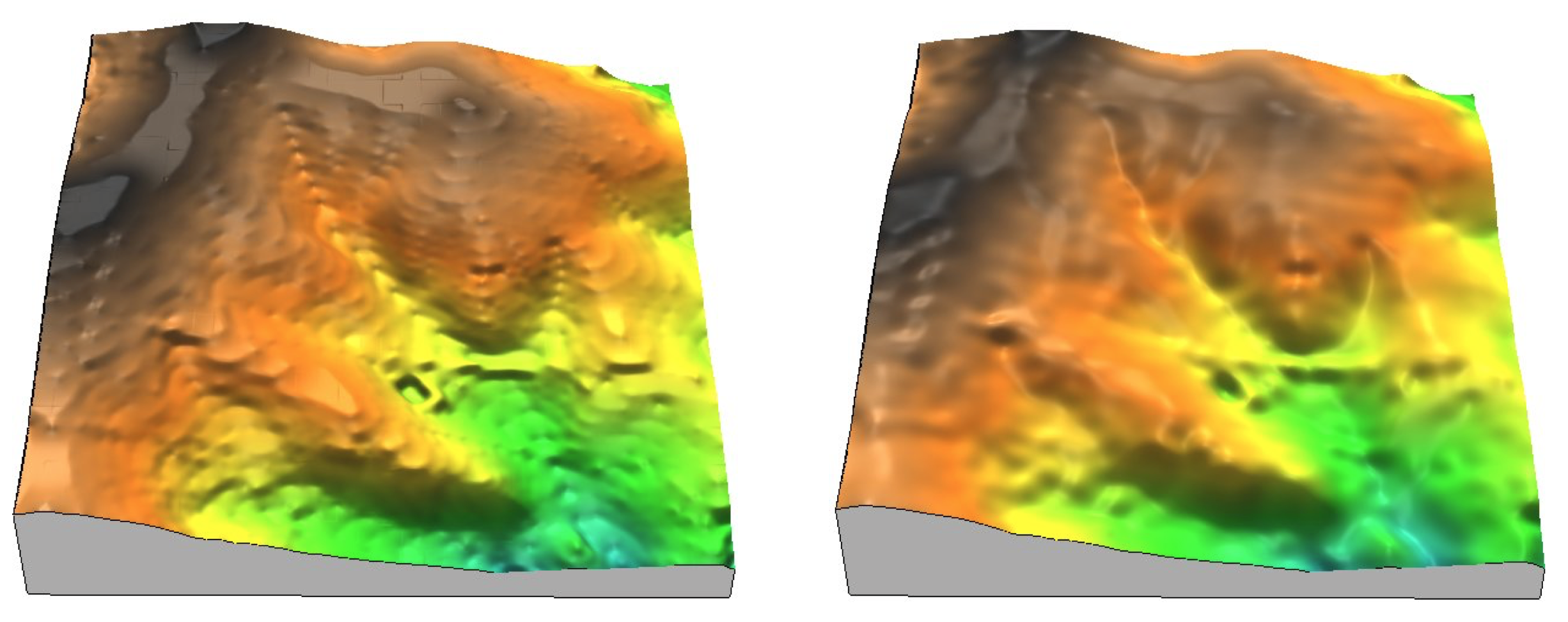
Trivariate Interpolation: tension
Impact of tension on the volume model: high to low

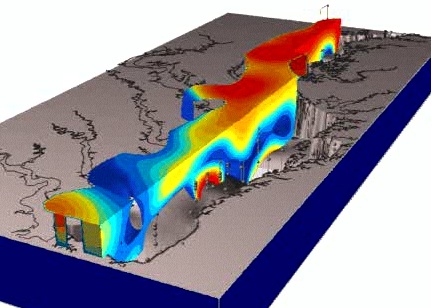
Mitas, L., Mitasova, H., 1999, Spatial Interpolation. GeoInformation International, Wiley, 481-492.
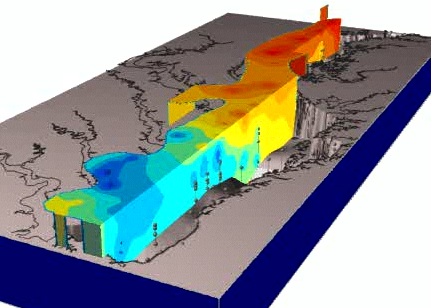
Trivariate Interpolation: tension
Impact of tension on the volume model
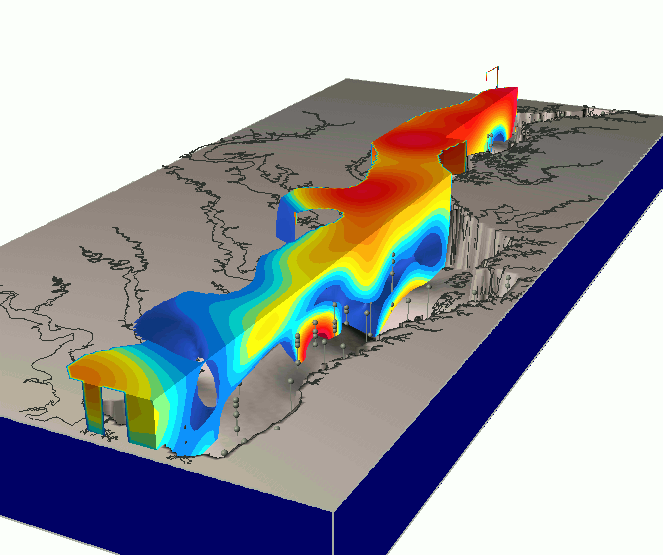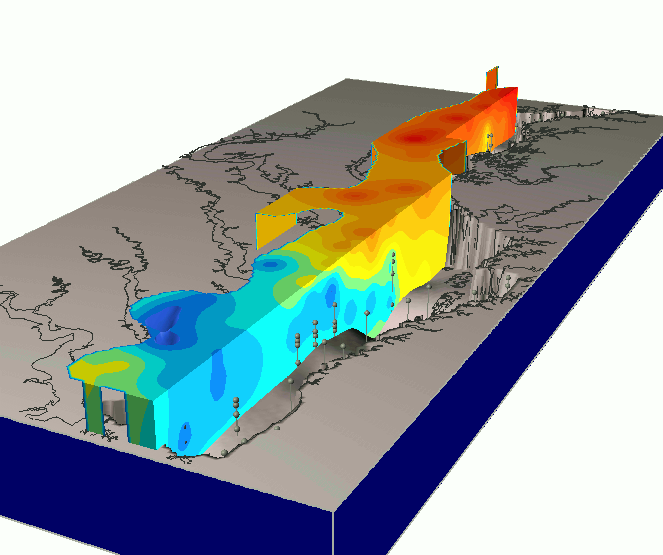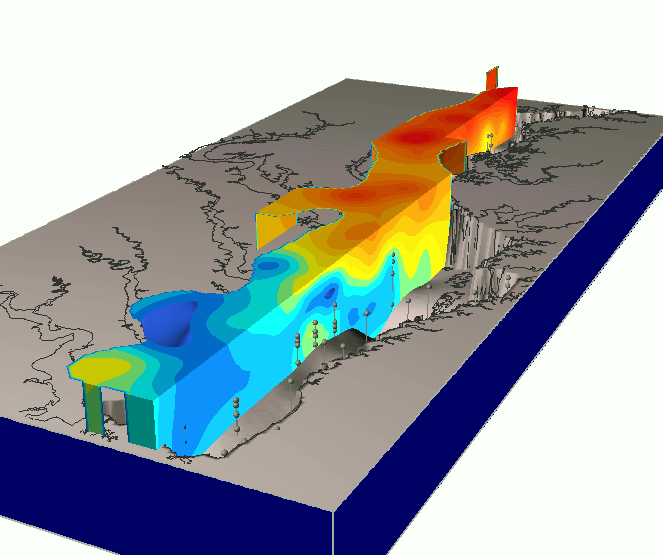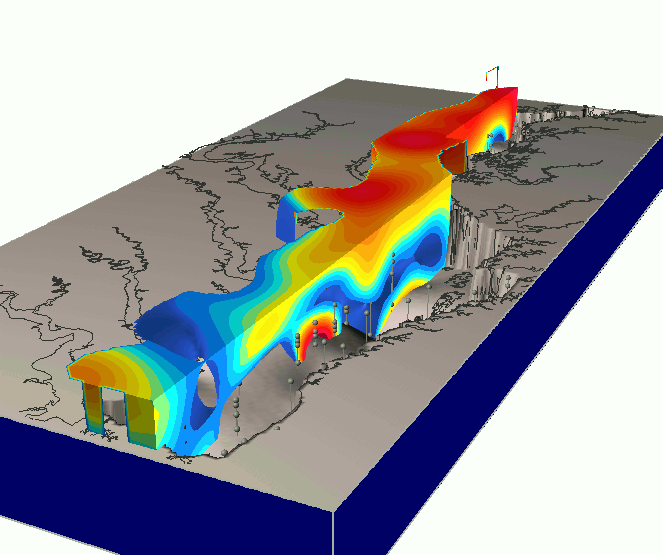

High tension: local maxima or minima at given points; low tension: smooth pattern with potential "overshoots"
Mitas, L., Mitasova, H., 1999, Spatial Interpolation. GeoInformation International, Wiley, 481-492.
Trivariate Interpolation to 2D grid
- Interpolation of 2D grid with influence of third variable
- Given $m$ points $(x_i,y_i,z_i,w_i)$ where $z_i = F_1 (x_i,y_i)$ find such $F_2(x,y,z)$ that for each $i=1,m$ $$ w_i=F_2(x_i,y_i,z_i) $$
- then compute $w_k=F_3(x_k,y_k)$ at $F_1 \cap F_2$
- Example: $w_i$ is precipitation measured at locations $x_i,y_i$ at ground elevation $z_i$. $F_1$ is represented by a DEM, $F_2$ is an interpolated precipitation volume (voxel model) that passes through the points $(x_i,y_i,z_i,w_i)$. $F_3$ is a bivariate function represented as a 2D precipitation grid which is an intersection of a DEM and the interpolated precipitation volume $F_2$
- Statistical approach of the method is described in Hutchinson, MF, 1995, Interpolating mean rainfall using thin plate smoothing splines, Int. Journal of Geographical Information Systems 9(4), 385-403. and has been used to interpolate global climate maps
- See also Hofierka J., et al. 2002, Multivariate Interpolation of Precipitation Using Regularized Spline with Tension. TGIS 6(2), 135-150.
Trivariate Interpolation: precipitation
NC mean annual precipitation with zoom into Western NC: bivariate interpolation and trivariate interpolation which includes influence of elevation
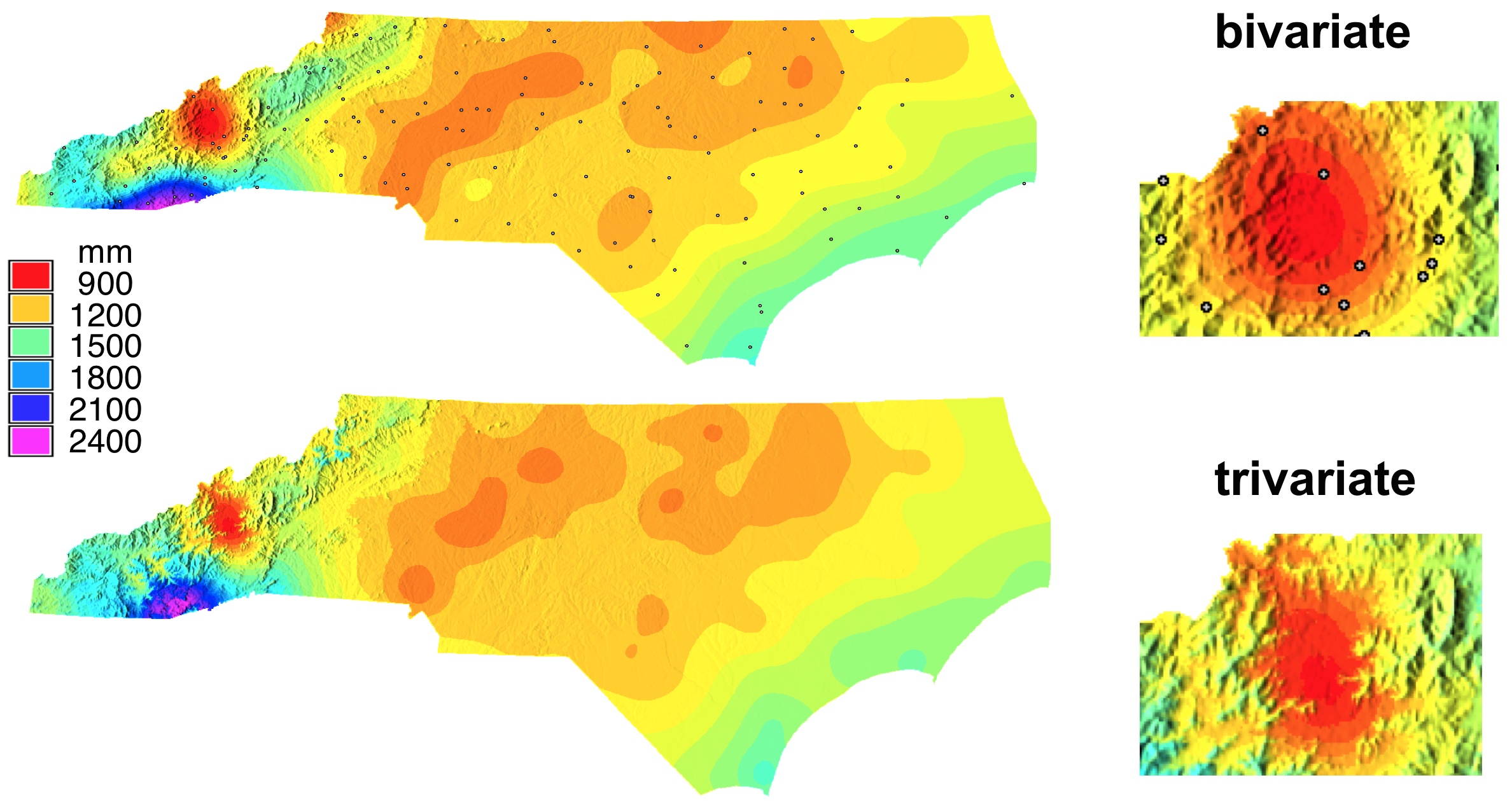
If sufficient data are available, the method captures increase of precipitation
with elevation around Asheville and decrease of precipitation with elevation on the border with SC
Trivariate Interpolation: precipitation
Tropical South America mean annual precipitation using bivariate and trivariate interpolation
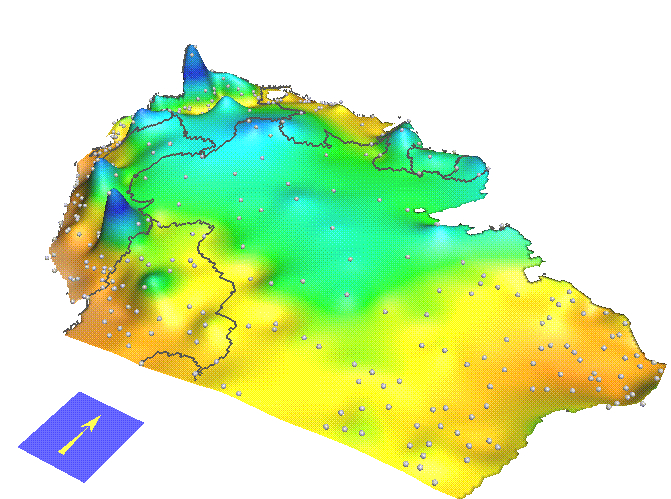
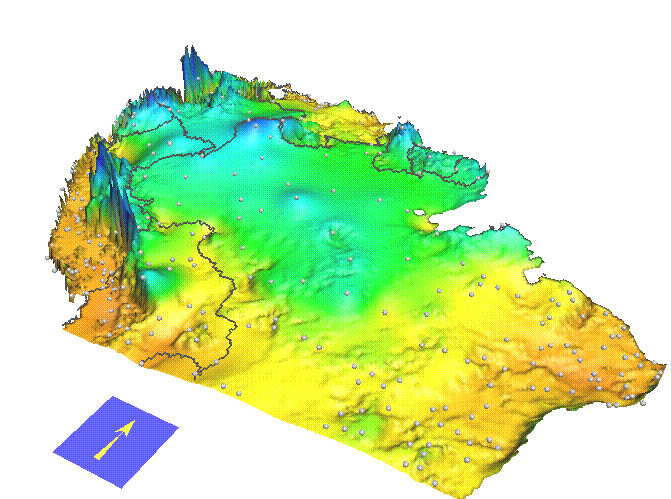
Mitas, L., Mitasova, H., 1999, Spatial Interpolation. GeoInformation International, Wiley, 481-492.
Trivariate Interpolation: precipitation
Tuning the influence of elevation on precipitation pattern through rescaling in the $z$-direction
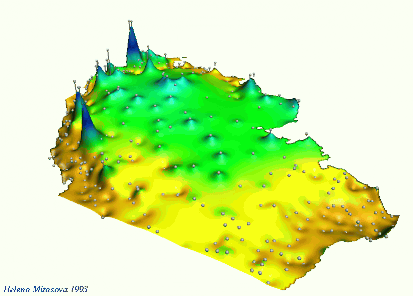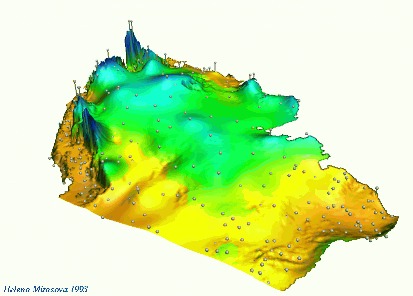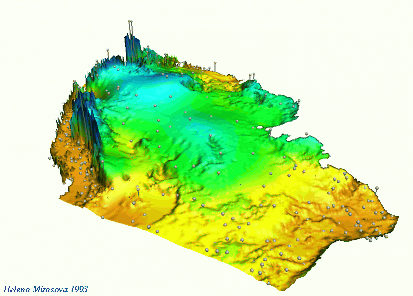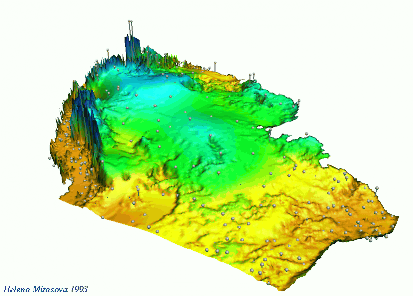

Mitas, L., Mitasova, H., 1999, Spatial Interpolation. GeoInformation International, Wiley, 481-492.
Quad-variate spline interpolation
Dynamics of nitrogen concentrations during a year, based on monthly measurements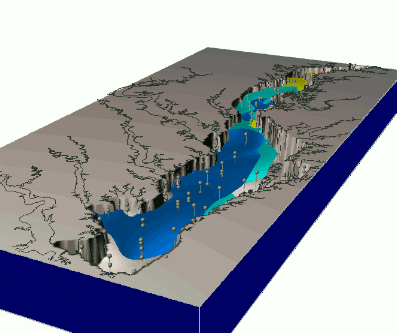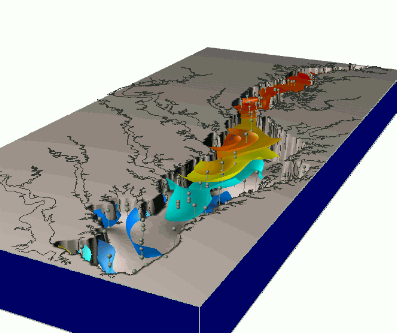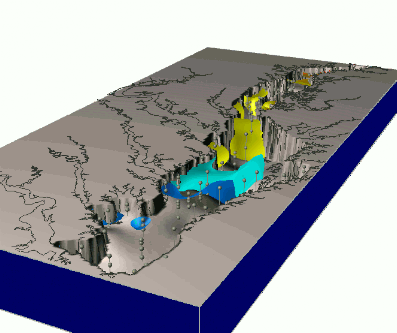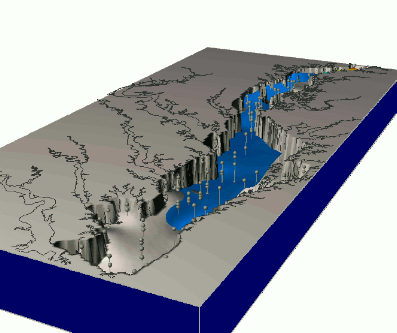

Quad-variate spline interpolation
Dynamics of groundwater contamination over 10 years

Summary
- Spline interpolation and its parameters: tension and smoothing
- Evaluating interpolation accuracy: deviations, crossvalidation
- Special cases: contours, anisotropy
- Processing large point data sets: segmentation, subsampling
- Multivariate interpolation: volumes, topo-climatology, dynamic volumes