FUTURES

FUTure Urban-Regional Environment Simulation

Anna Petrasova, Vaclav Petras

GIS714 Geosimulations NCSU

FUTURES

(Meentemeyer et al., 2013)

  • urban growth model
  • patch-based
  • stochastic
  • accounts for location, quantity, and pattern of change
  • positive feedbacks (new development attracts more development)
  • allows spatial non-stationarity

FUTURES, A Simplified View

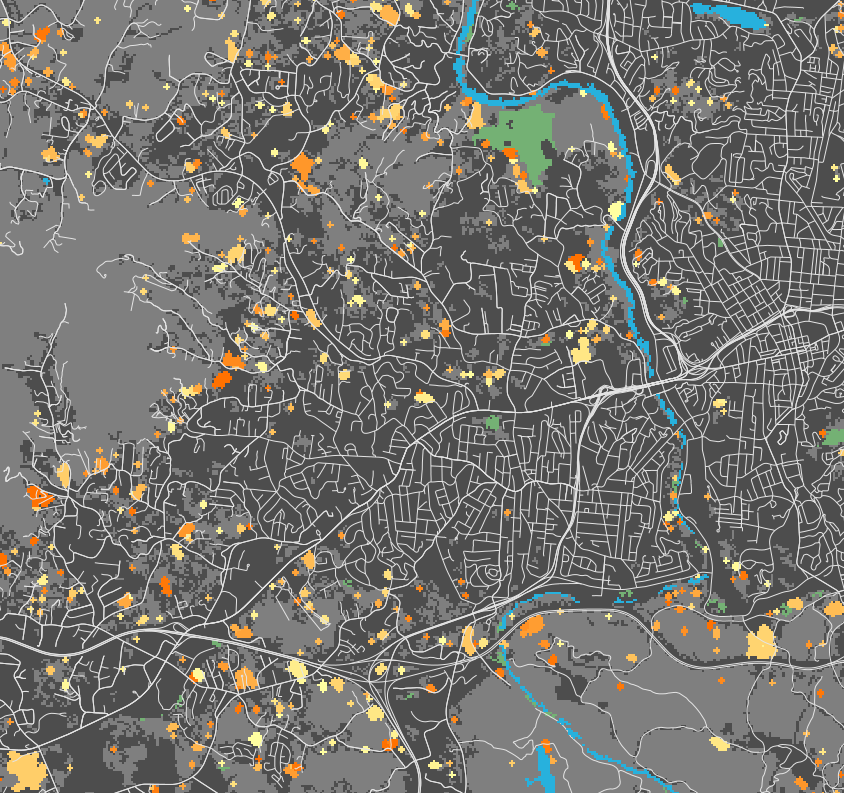
turning green cells into orange cells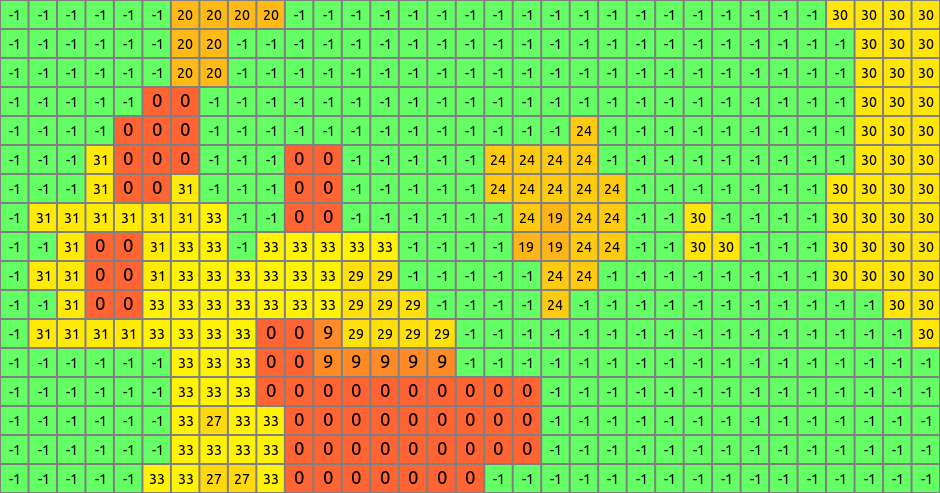

-1: undeveloped, 0: initial development, 1: developed in the first year, …

Modeling framework

Demand submodel

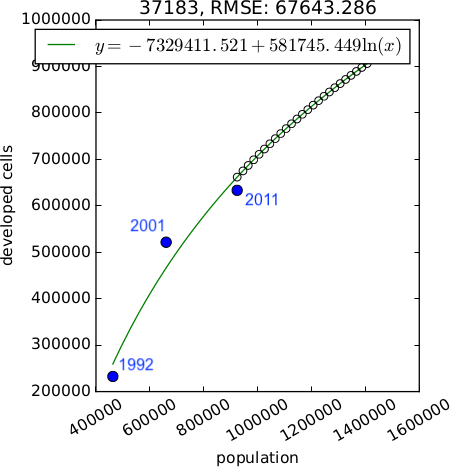
  • estimates the rate of per capita land consumption for each subregion
  • extrapolates between historical changes in population and land conversion
  • inputs are historical landuse, population data, population projection

Demand scenarios

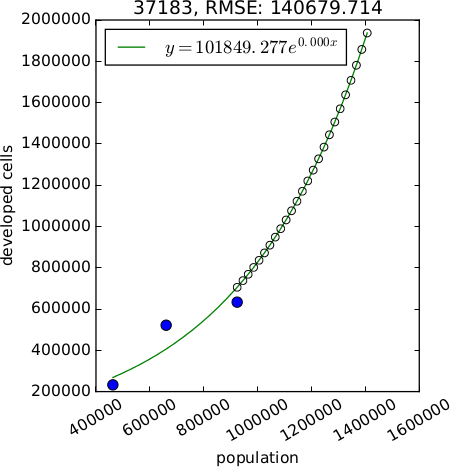
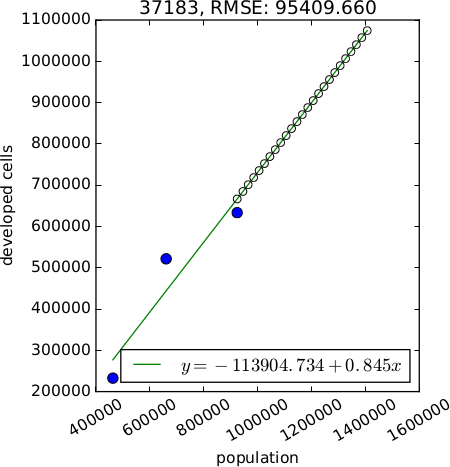
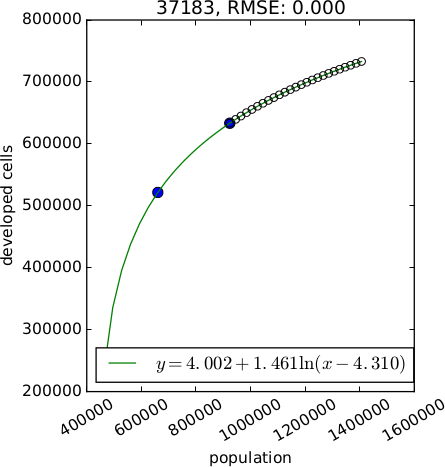
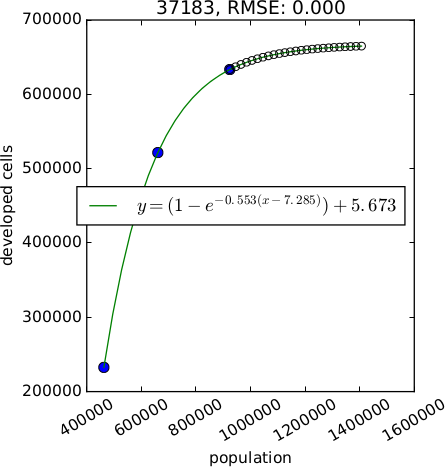
$$ y = Ae^{BX} \\ y = A + Bx \\ y = A + B ln(x) \\ y = A + B ln(x - C) \\ y = (1 - e^{-A(x - B)}) + C $$

Demand: population decline

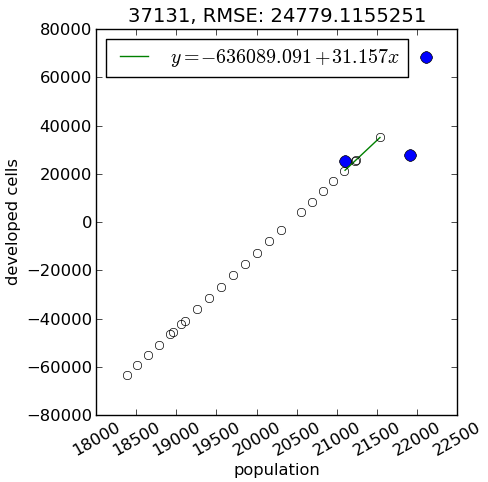
  • demand submodel designed for regions with population growth
  • FUTURES doesn't simulate cell de-conversion: here it would simulate zero new cell conversions
  • even with population decline, impervious areas can increase

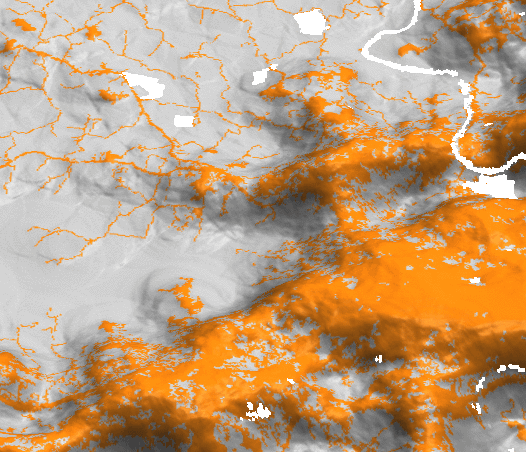
Potential submodel

  • multilevel logistic regression for development suitability accounts for variation among subregions (for example policies in different counties)
  • inputs are uncorrelated predictors (distance to roads and development, slope, ...)

surface: potential, orange: developed areas, green: undeveloped areas

Potential submodel

$$ p_i = \frac{e^{s_i}}{1 + e^{s_i}} $$ $p_i$ is development probability for cell i,
$s_i$ is development potential for cell i
$$ s_i = a_{j,i} + \sum_{h=1}^{n} \beta_{j, i, h} \, x_{i, h} $$ $j$ is the level (e.g. counties),
$h$ is a predictor,
$n$ is the number of predictor variables,
$a_{j,i}$ is intercept,
$\beta_{j, i, h}$ is regression coefficient,
$x_{ih}$ is the value of h at i

Potential submodel: workflow

  1. stratified random sampling of predictors and response variable (developed/undeveloped raster)
  2. glm(developed ~ (1|subregion) + distance_to_water + development_pressure + road_density + ...)
    • using automatic selection based on AIC
  3. create probability surface from regression coefficients

Potential submodel: notes

  • predictors and coefficients do not change during simulation (except for development pressure)
  • avoid multicollinearity

Development pressure

  • Predictor based on number of neighboring developed cells within search distance, weighted by distance.
  • Allows for a feedback between predicted change and change in subsequent steps.
$$pressure = \sum^{n_i}_{k=1} \frac{state_k} {d^{\gamma}_{ik}}$$
where $state_k$ indicates whether $k$th neighboring cell is 1 or 0 (developed or undeveloped)
$d_{ik}$ is distance between current cell $i$ and neighboring cell $k$
and $\gamma$ controls the influence of distance between neighboring cells

Development pressure

Patch Growing Algorithm

  • stochastic algorithm
  • converts land in discrete patches
  • inputs are patch characteristics (distribution of patch sizes and compactness) derived from historical data

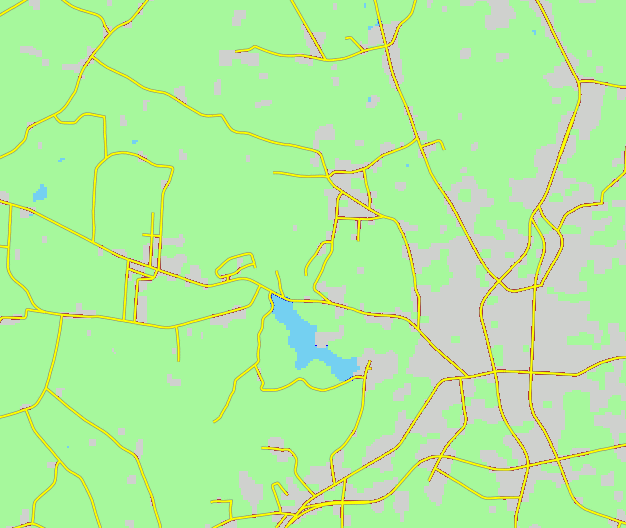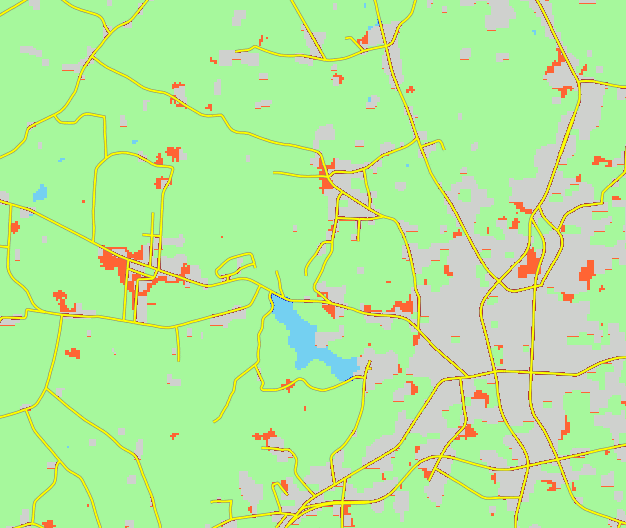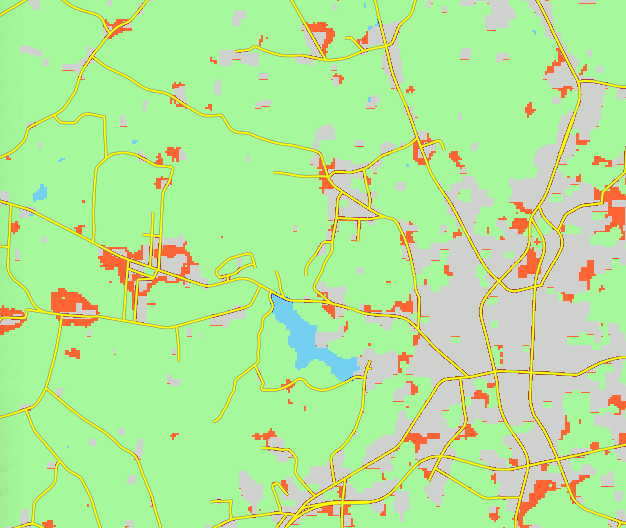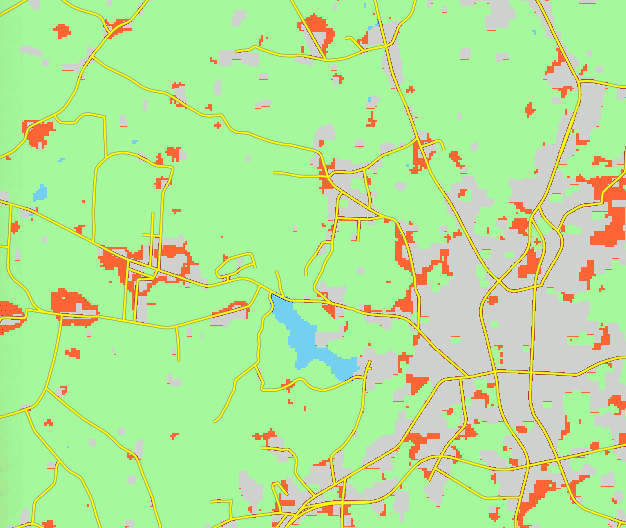
Patch Growing Algorithm

  1. pick randomly a seed cell $i$
  2. seed is established if $p_i$ > random number
  3. randomly pick patch size
  4. grow patch
    1. add neighbors to a list and sort it based on $p_i / d^c$, where $d$ is distance from $i$ and $c$ is compactness value
    2. pick first neighboring cell and try to add it to the patch if $p_i$ > random number
    3. if added, add surrounding neighboring cells to the list
    4. repeat until the patch size is met
  5. recompute development pressure

Patch Compactness

Low
High

Scenarios: Incentive power


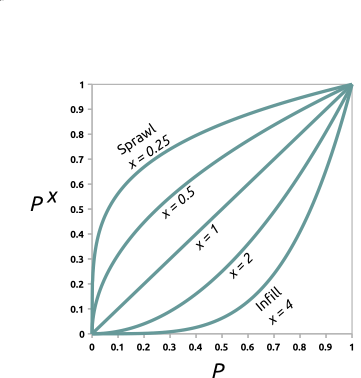
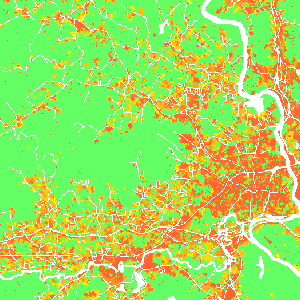
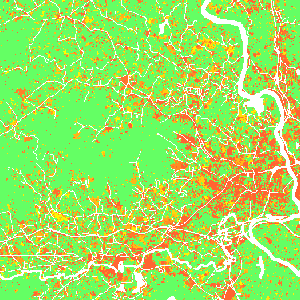
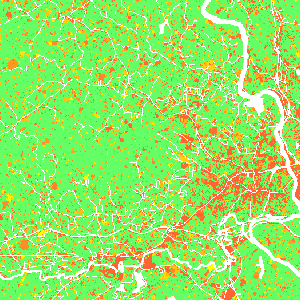
Scenarios

Constraint parameter: zones with decreased probability of development $$P_{new} = P . C, \quad C \in \langle 0, 1\rangle $$
Stimulus parameter: zones with increased probability of development $$P_{new} = P + S - P.S, \quad S \in \langle 0, 1 \rangle$$

r.futures

Information flow diagram for the set of modules implementing FUTURES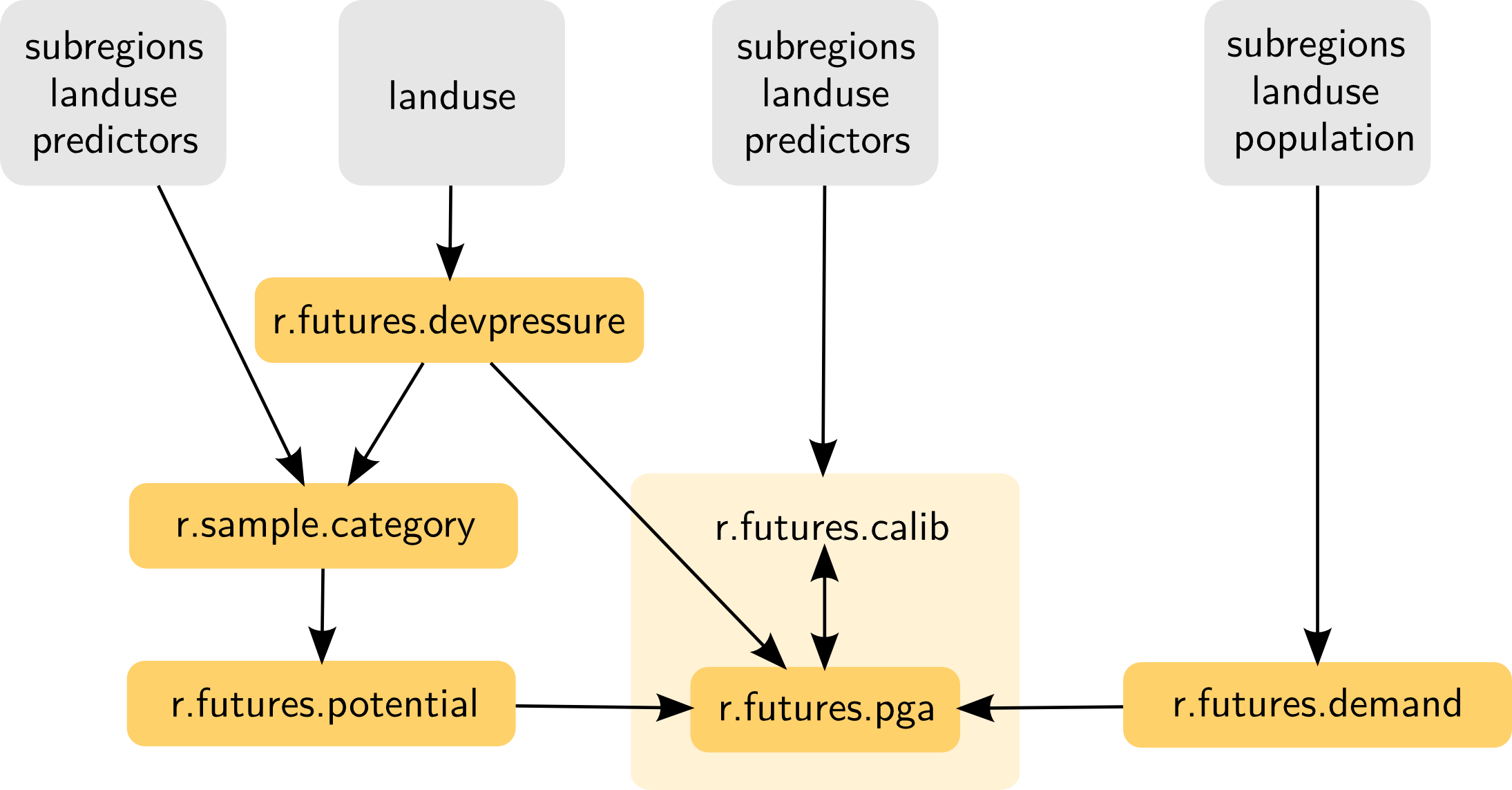

Additionally, r.futures.parallelpga can be used instead of r.futures.pga.

⌂