Data simulation

Helena Mitasova, Anna Petrasova, Vaclav Petras

GIS714 Geosimulations NCSU

Learning objectives

  • when we need data simulation
  • deterministic, random, and fractal surfaces
  • simulating point data and patches
  • generating scenarios

Steps in development of simulations

  • definition of research question
  • identification of available data
  • design or identification of modeling approach suitable for the research question and available data recall:modeling quantity,scale,configuration space and interactions, governing equations
  • sensitivity analysis (most important parameters)
  • model parametrization
  • calibration and validation
  • generating scenarios and running simulations
  • uncertainty analysis and error propagation

Motivation for simulating data

  • sensitivity analysis: generating model parameters
  • uncertainty analysis: simulating errors
  • scenario modeling
  • testing algorithms
  • noise and artifact detection

Types of simulated data

  • Geometry

    • points, lines, areas, rasters, surfaces
    • synthetic data sets - time series

  • Approach

    • deterministic
    • stochastic
    • hybrid

Geometry based spatial methods

Deterministic: mathematical functions

$z = 0.2 x + 0.02 y + 50$

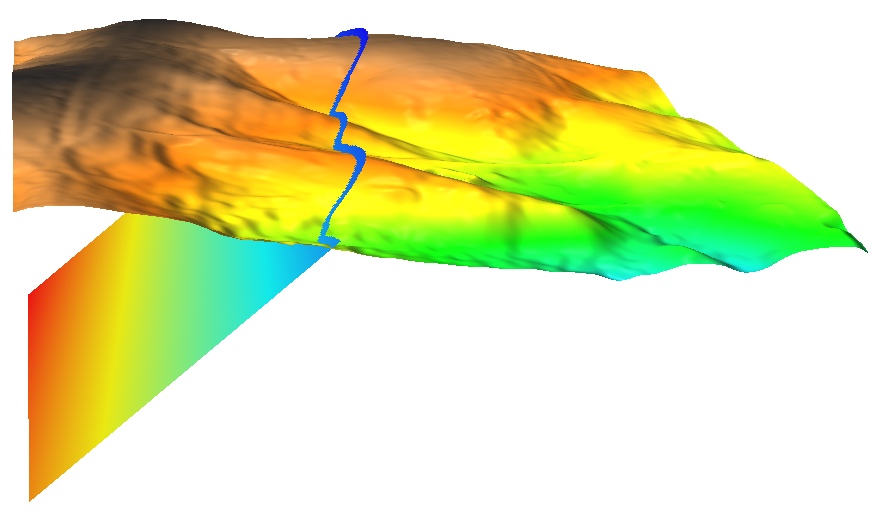
Geometry based spatial methods

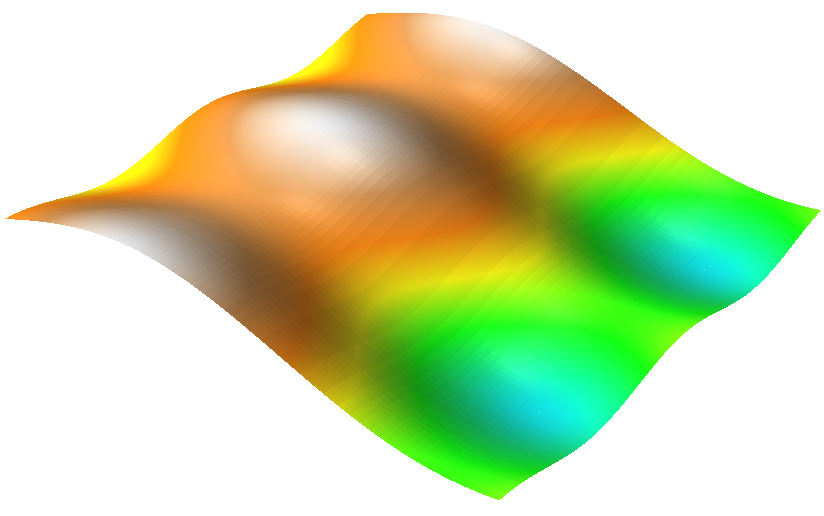
Deterministic: mathematical functions

$z = \sin (0.4x) + 0.3 \cos(y) + 80$

Smooth, simplified surface

Stochastic methods

  • Methods based on random fields
  • Uniform random field - linear random number generator


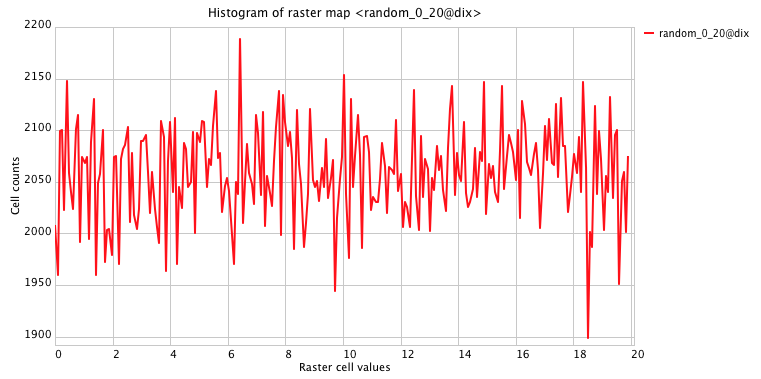
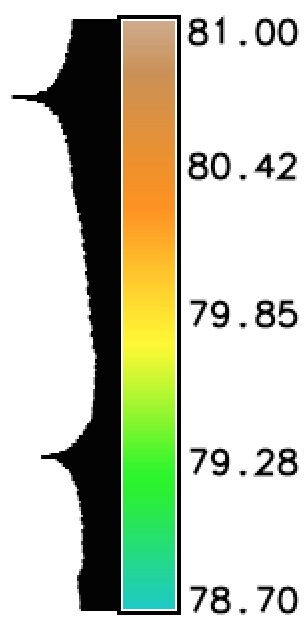
Random numbers from interval [0,20], mean=10: surface and histogram

Stochastic methods

Independent random variable $z$, is often distributed according to the normal distribution: $$ f(z | \mu,\sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} e^{-(z-\mu)^2 / 2\sigma^2} $$

where $\mu$ is the mean, $\sigma$ is the standard deviation, $\sigma^2$ is the variance, $e$ is exponential function, and $f(z | \mu,\sigma^2)$ is probability density function of the normal distribution

Monte Carlo methods often require generating values that have normal distribution

Learn more about Normal distribution

Gaussian random field

Random field with $\mu = 120$m and $\sigma = 2$m

One $\sigma$ (68%) of values in the random field are within 2m range of the mean

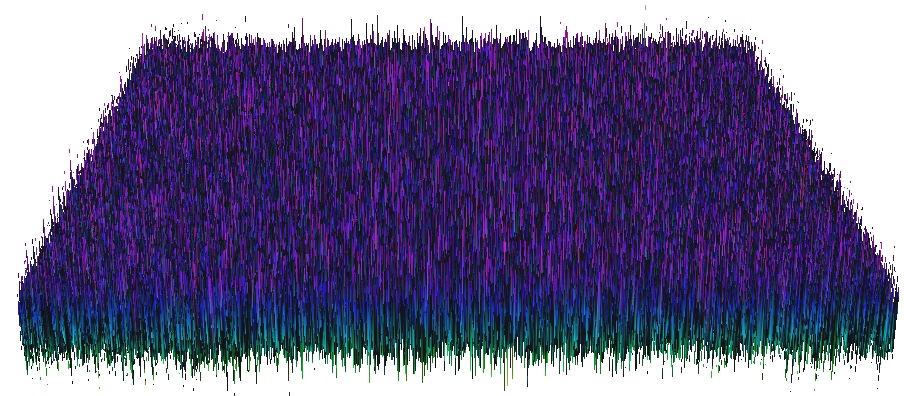
Uniform and Gaussian random fields

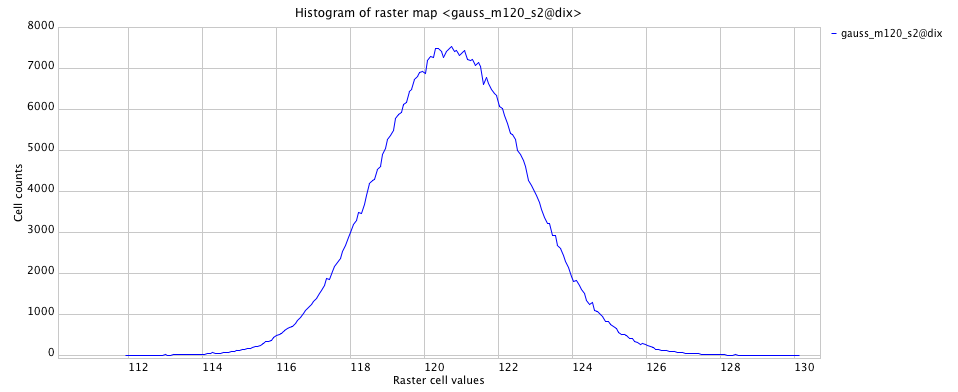
Profile and histograms of random fields:

uniform where $z = [0,20]$

Gaussian $z$ where $\mu = 10$ and $\sigma = 6$


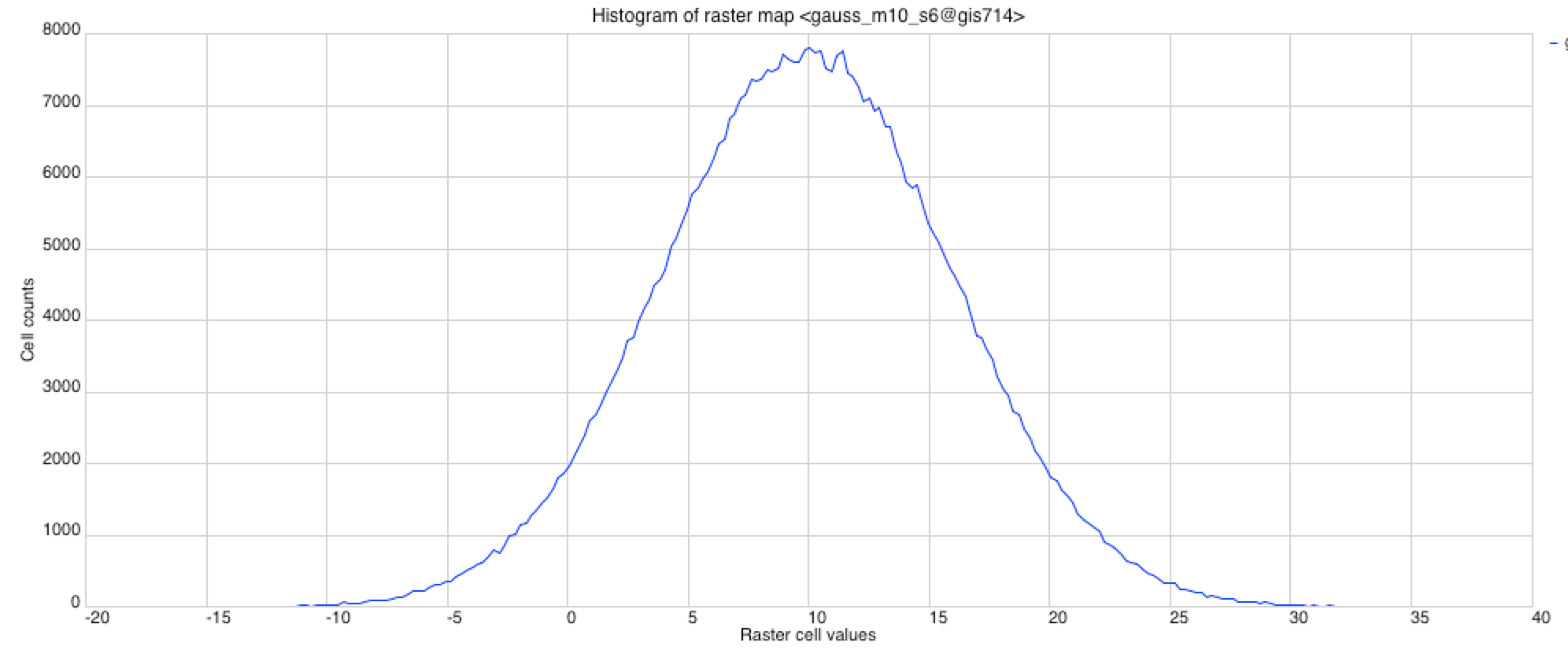
Uniform and Gaussian random fields

2D maps: uniform random field $z = [0,20]$ and Gaussian random field with $\mu = 10$ and $\sigma = 6$m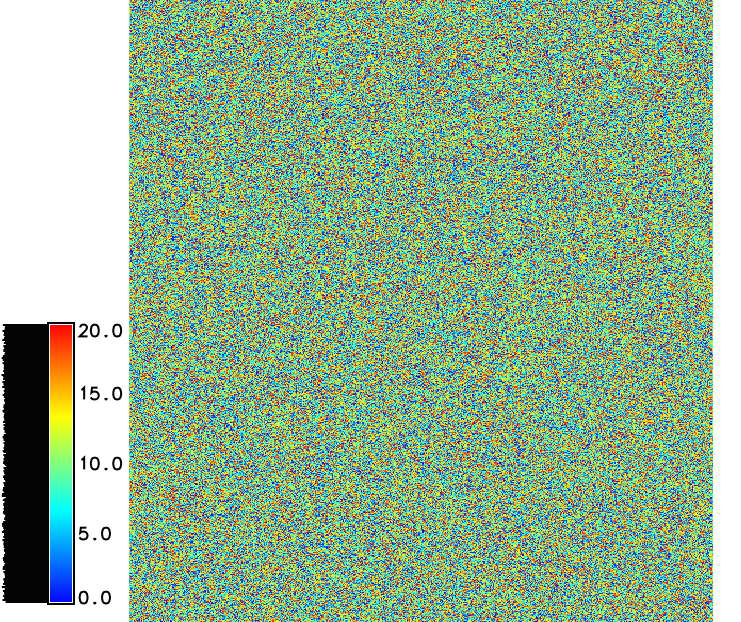

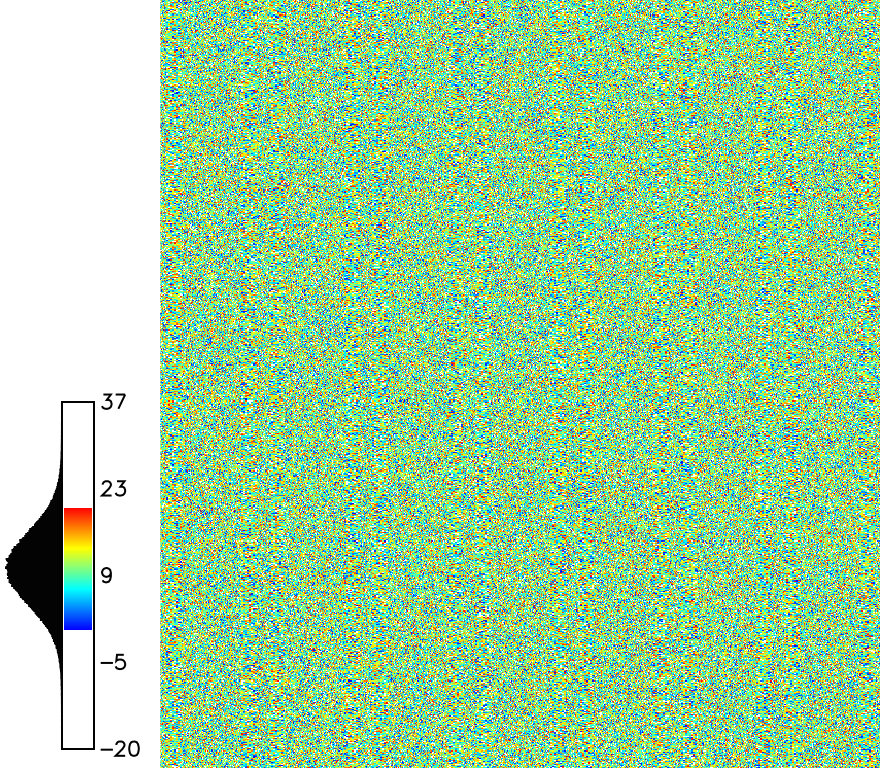
Simulation of random surface with spatial dependence

Initial Gaussian or uniform random field is smoothed based on a given filter

The filter defines the range and shape of spatial dependence

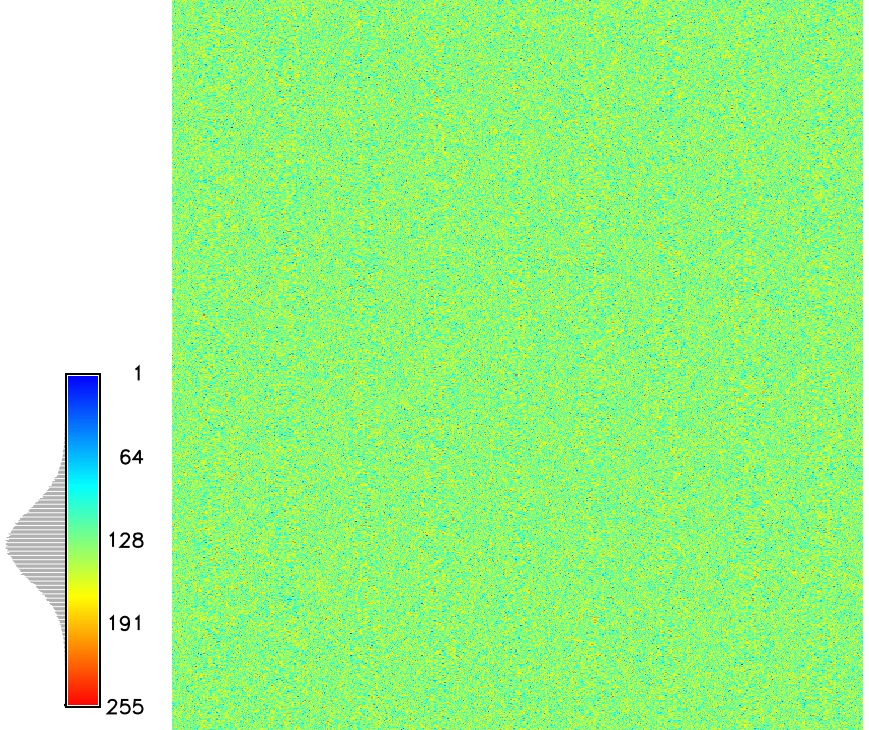
Spatial dependence

Gaussian random field - no spatial dependence

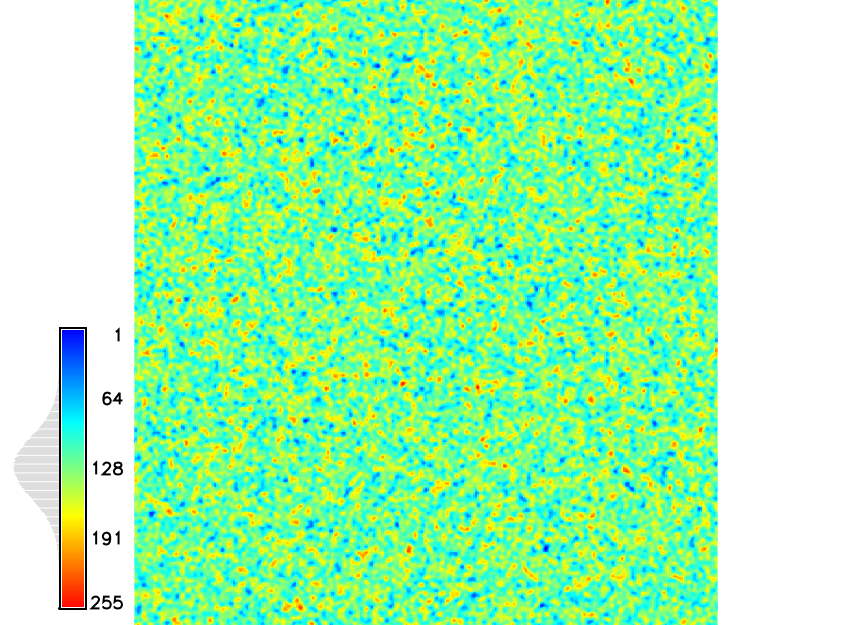
Spatial dependence

Gaussian random field with spatial dependence $d=10$

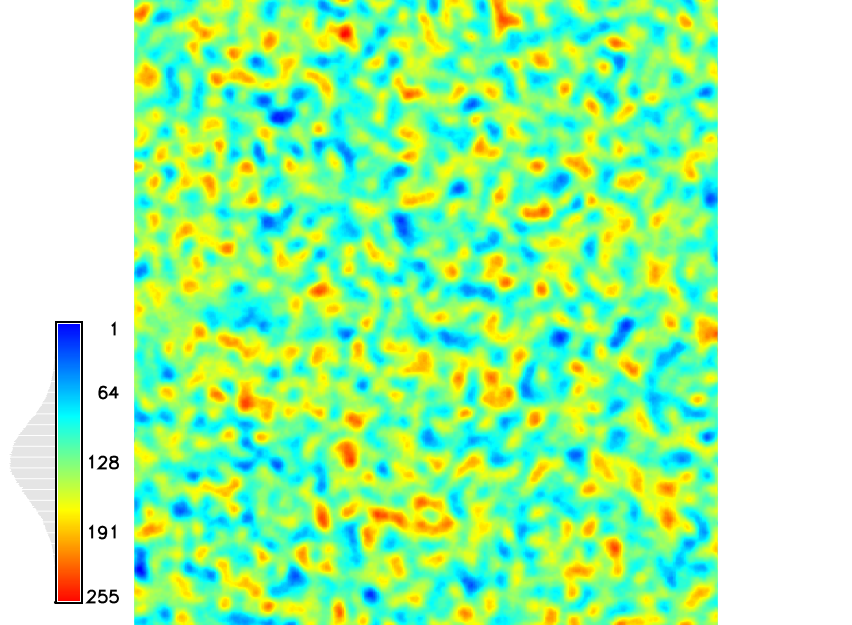
Spatial dependence

Gaussian random field spatial dependence $d=30$

Simulating random errors

Random gaussian field: $\mu = 0$m, $\sigma = 0.3$m
random measurement errors (noise)


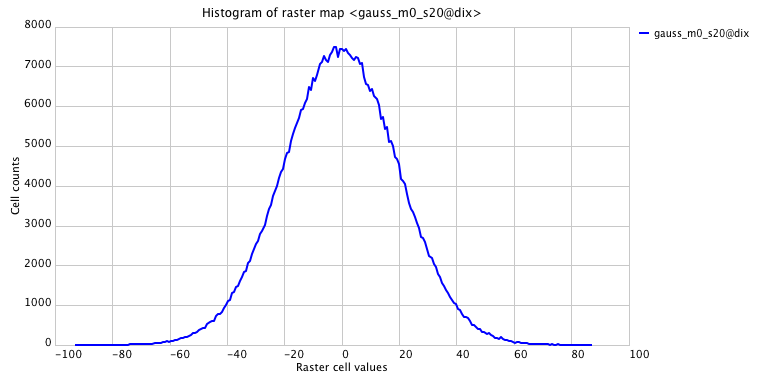
Simulation of DEM with noise

Initial elevation surface interpolated by smoothing splines

Simulation of DEM with noise

Gaussian random field with $\mu = 0$m and $\sigma = 0.3$m added to the elevation surface:

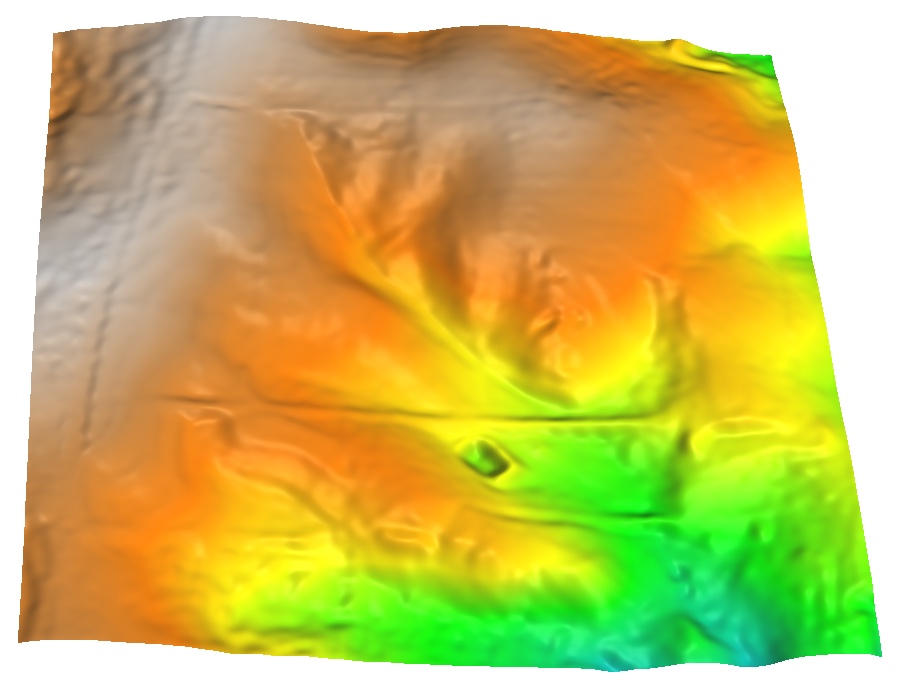
Simulation of DEM with noise

Gaussian random field with $\mu = 0$m and $\sigma = 0.3$m and spatial dependence d=10 added to the elevation surface:

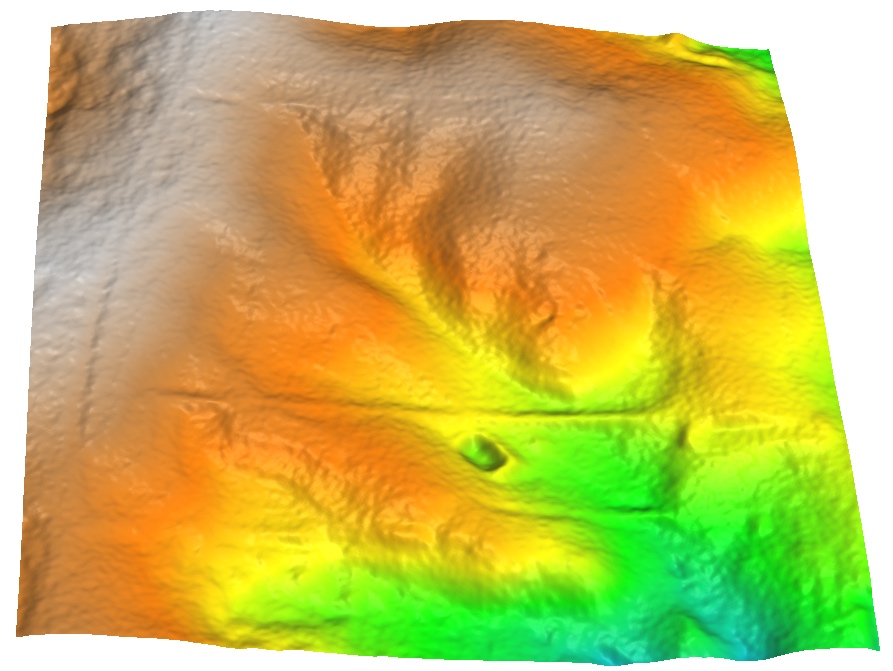
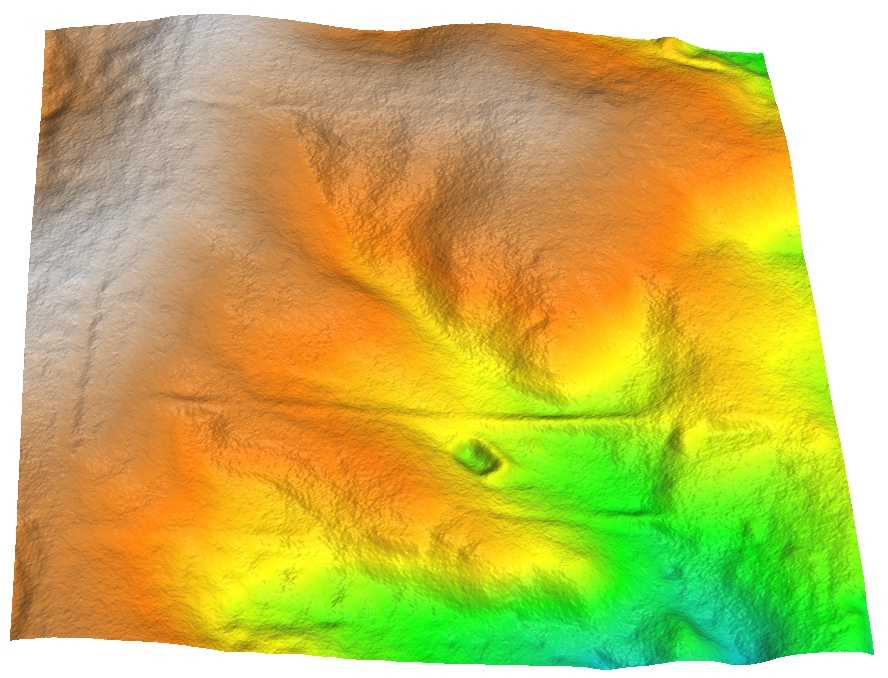
Simulation of DEM with noise

DEM interpolated from the lidar point cloud with limited smoothing

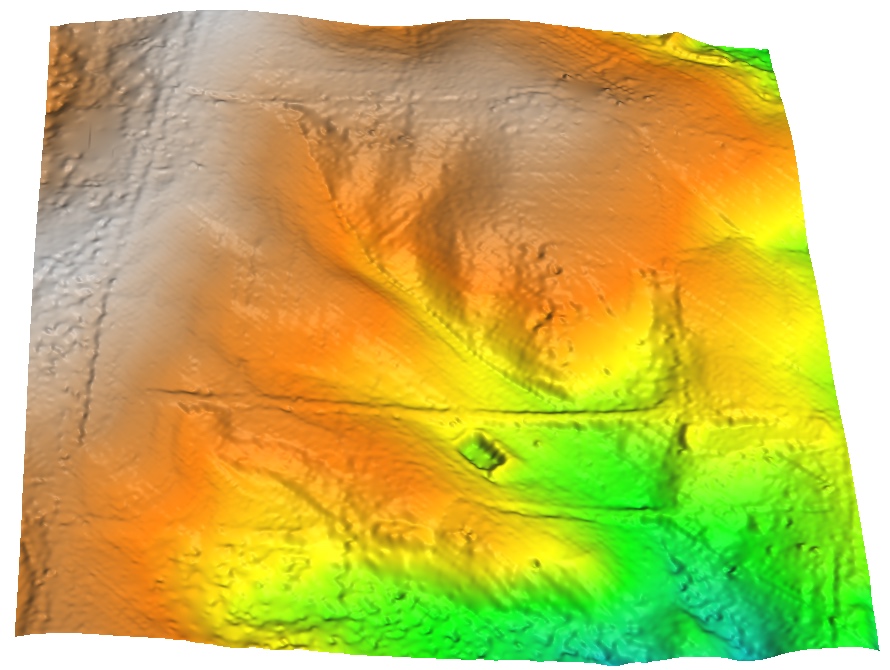
Flow over smooth DEM

Spatial pattern of surface flow over smooth DEM

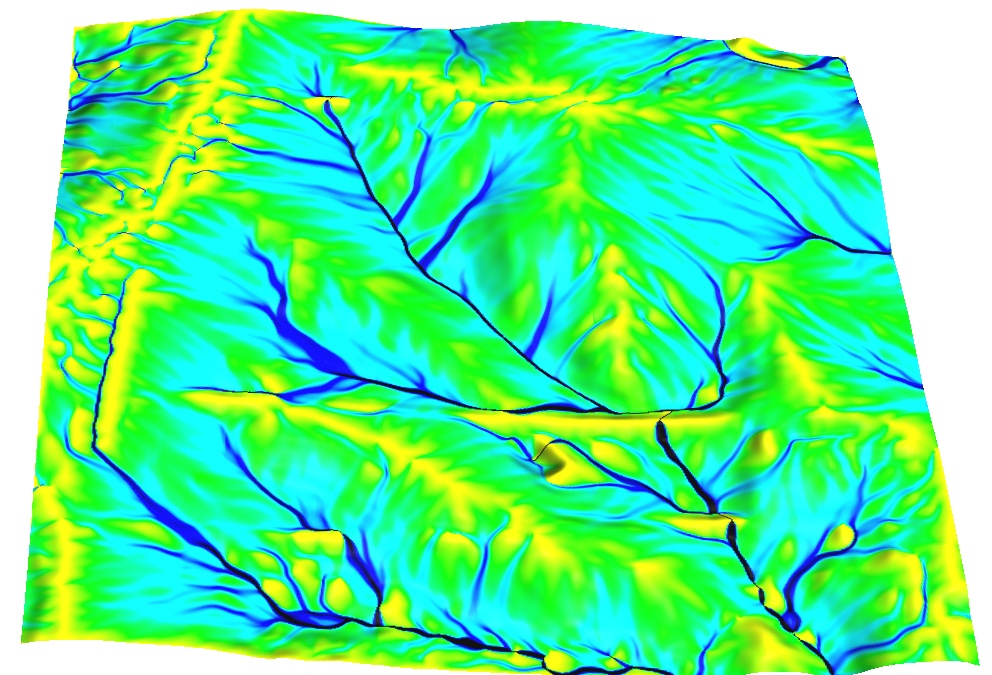
Flow over DEM with noise

Spatial pattern of surface flow over DEM with gaussian random noise

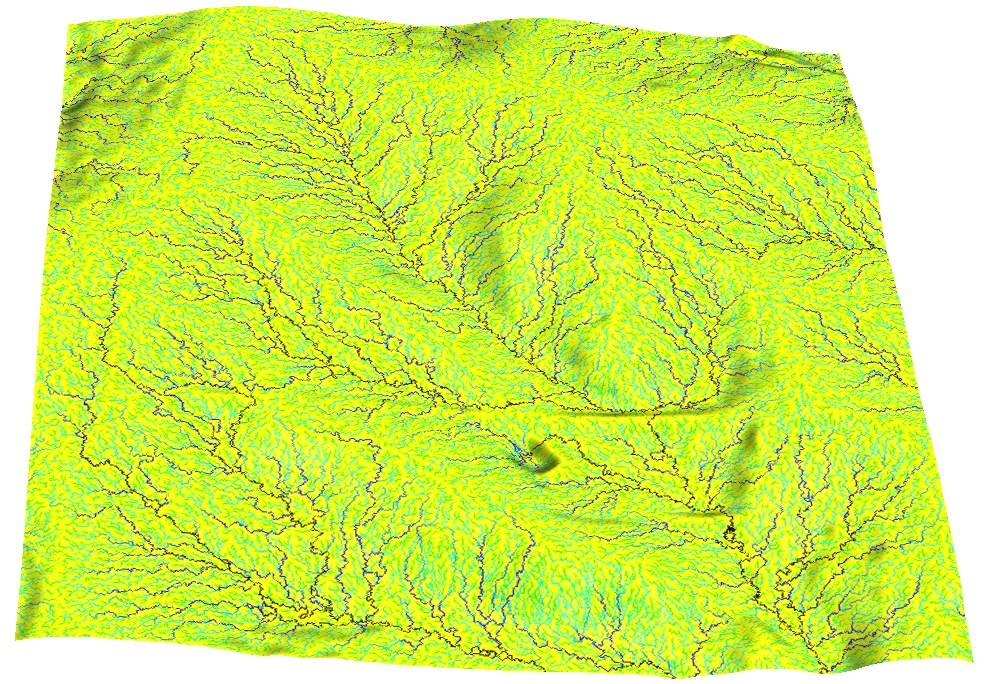
Flow over DEM with noise

Surface flow over noisy DEM with spatial dependency

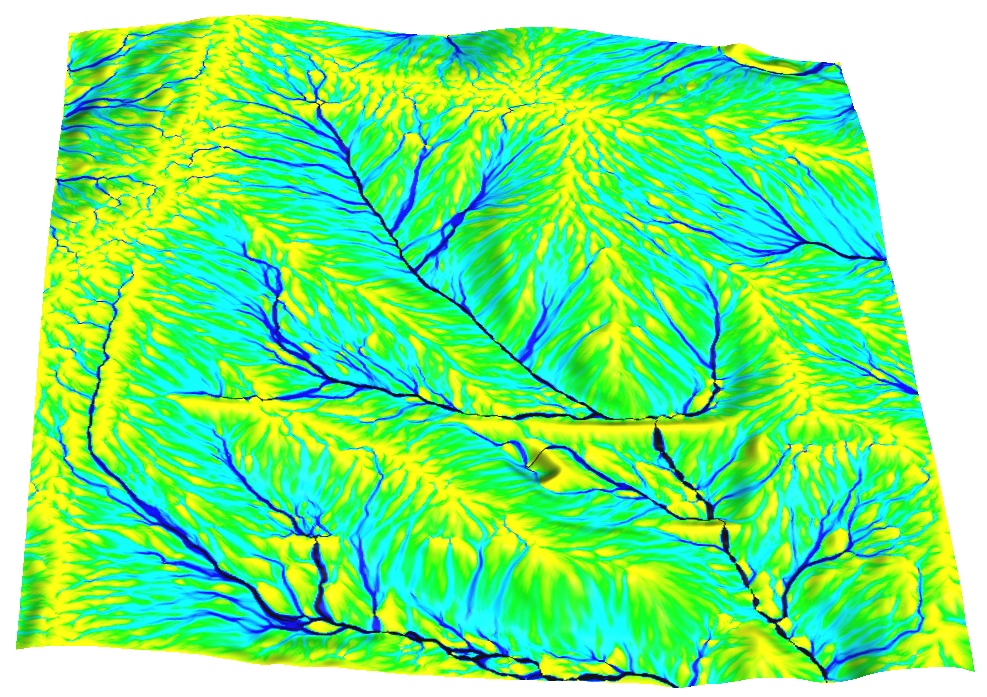
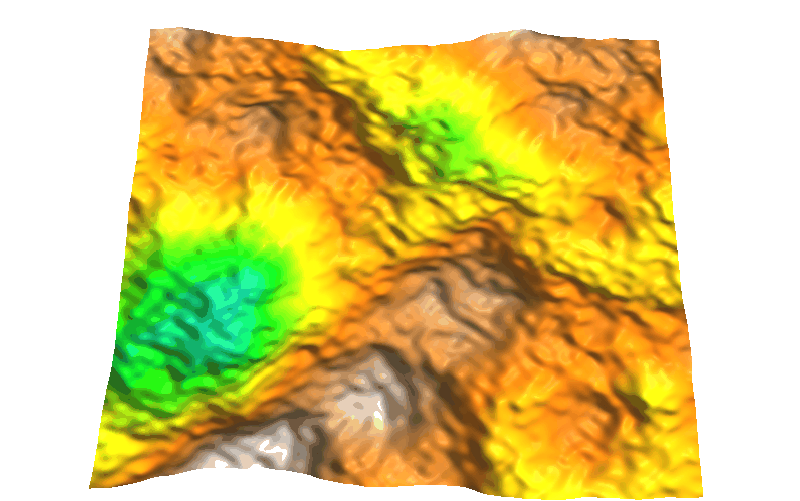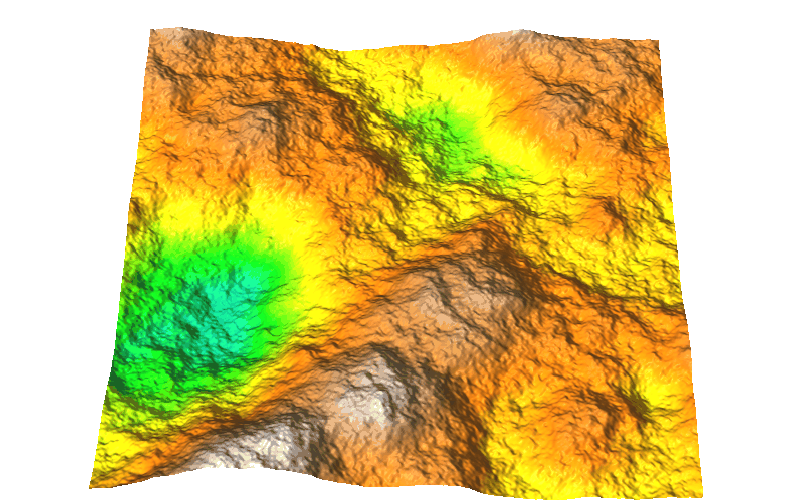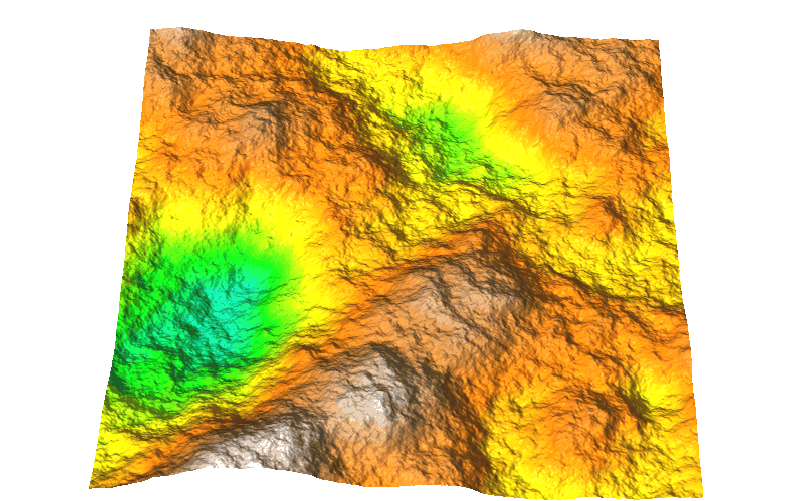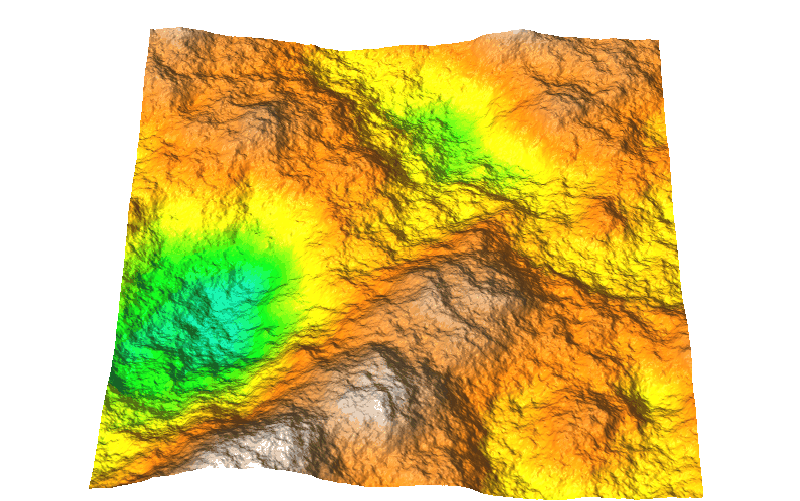
Flow over DEM with lidar noise

Surface flow over lidar-based DEM with NW-SE direction bias

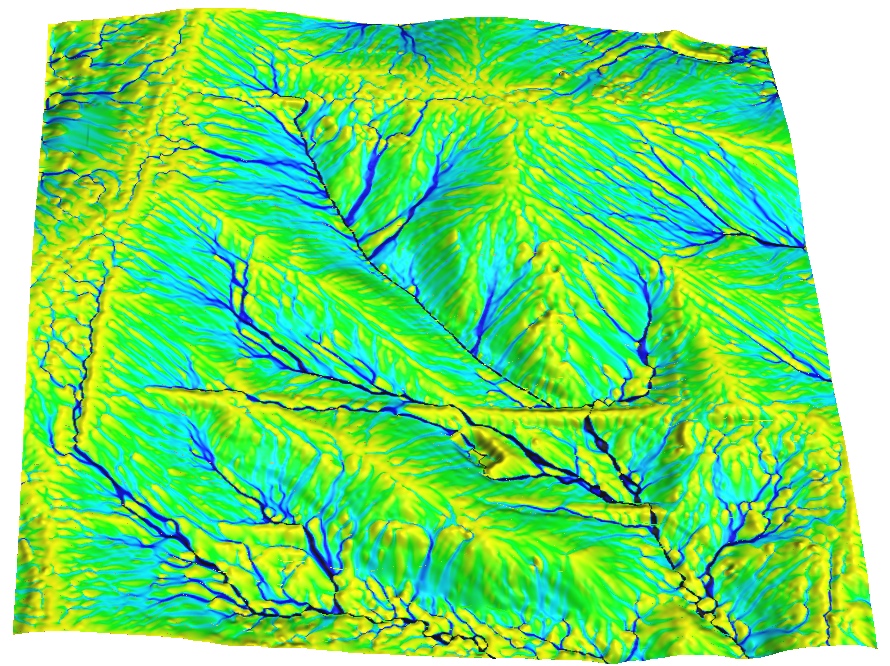
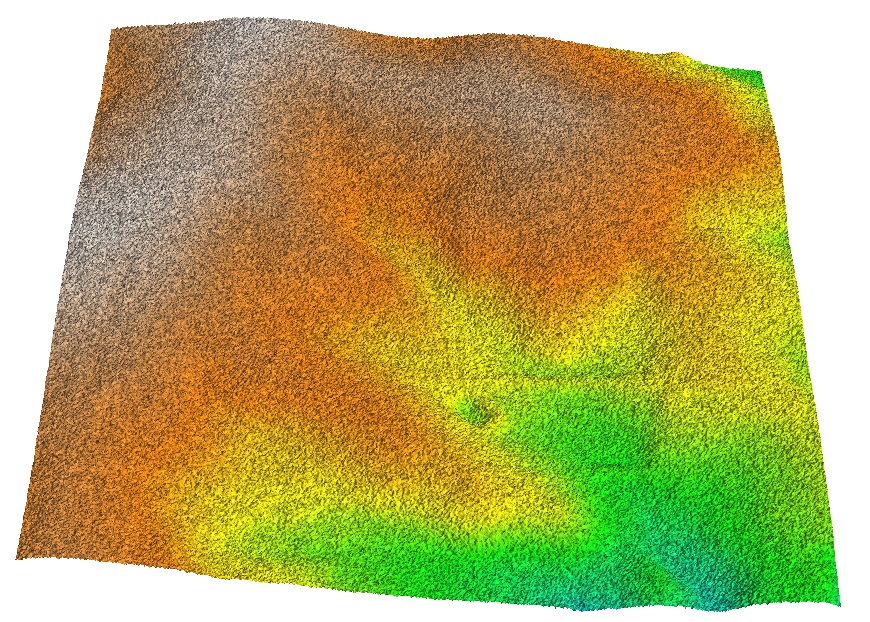
Lidar point cloud

Spatial pattern of bare ground lidar points

Fractals

Scale invariant features with infinite detail at all scales - complete computation of fractal is impossible

Fractals have non-integer dimension

Deterministic and random fractals

Deterministic fractals

  • Self-similar: scaled down and rotated copies of themselves
  • Simple algorithms: particular mappig is repeated in recursive scheme
  • Fractals by Hausdorff dimension

Random fractals

  • Include random component to simulate natural phenomena
  • Surfaces with no derivative (infinitely rough)
  • Fractal Brownian motion
  • Algorithms: midpoint displacement method, Fourier filtering method, random cut method

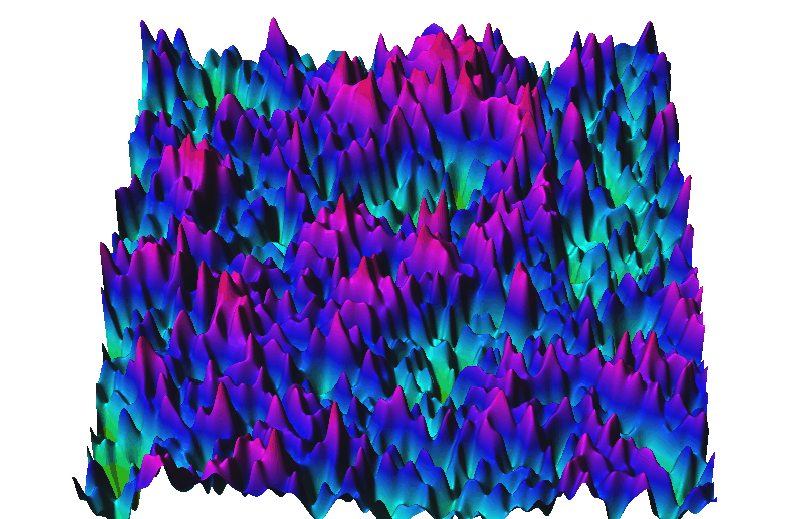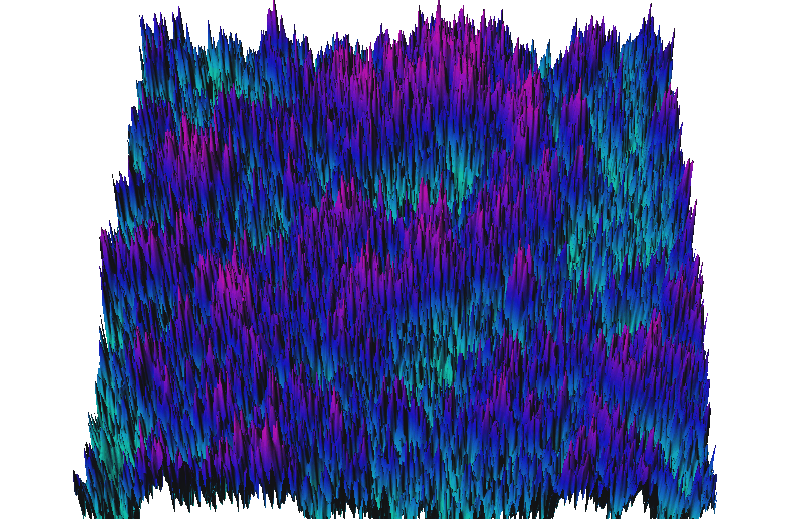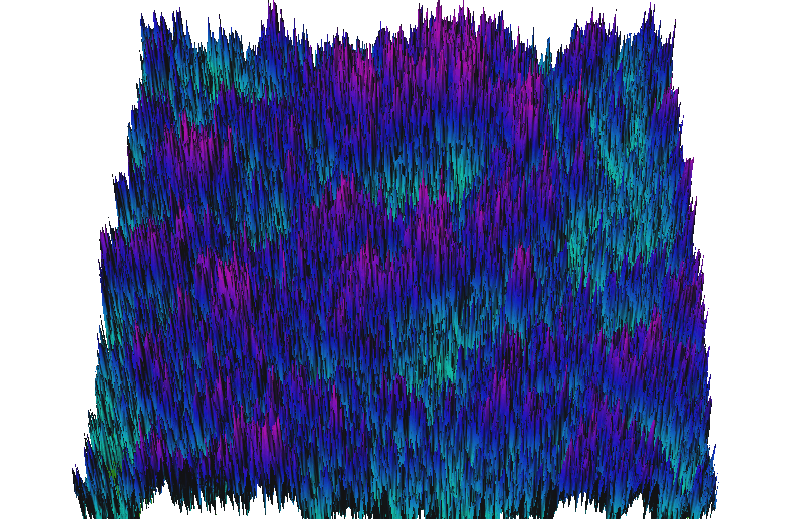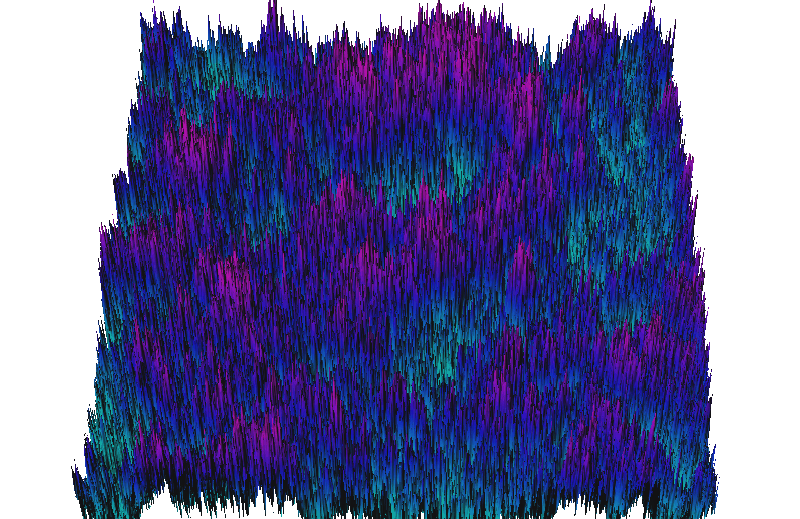
Random fractals

Surface generated by Fourier filtering method d=2.01

Random fractals

Surface generated by Fourier filtering method d=2.9

DEM with fractal-based noise

Fractal-based noise added to the elevation surface

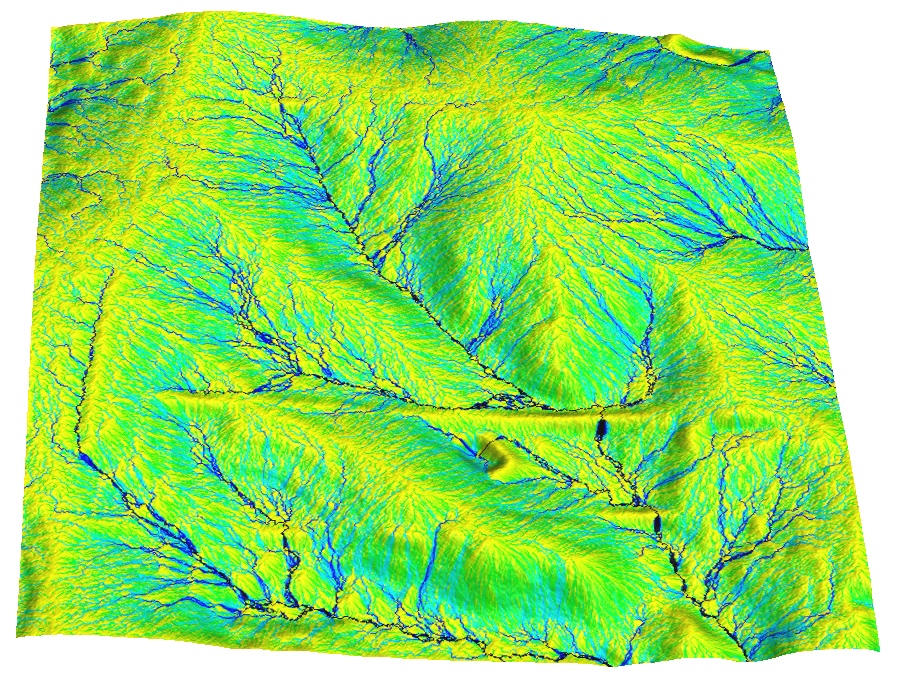
Flow over DEM with fractal noise

Spatial pattern of surface flow over lidar-based surface

Random points simulation and sampling

  • Randomly distributed points in a given space: coordinates $(x_i,y_i)$ are random numbers from a given distribution
  • Random points with spatial dependence - e.g. minimum distance appart
  • Random sampling of a given field, map, image
  • Stratified random sampling: preserves the distribution of values in the sampled data set
  • Perturbated random point fields
  • Random subsets of existing point data for calibration and validation

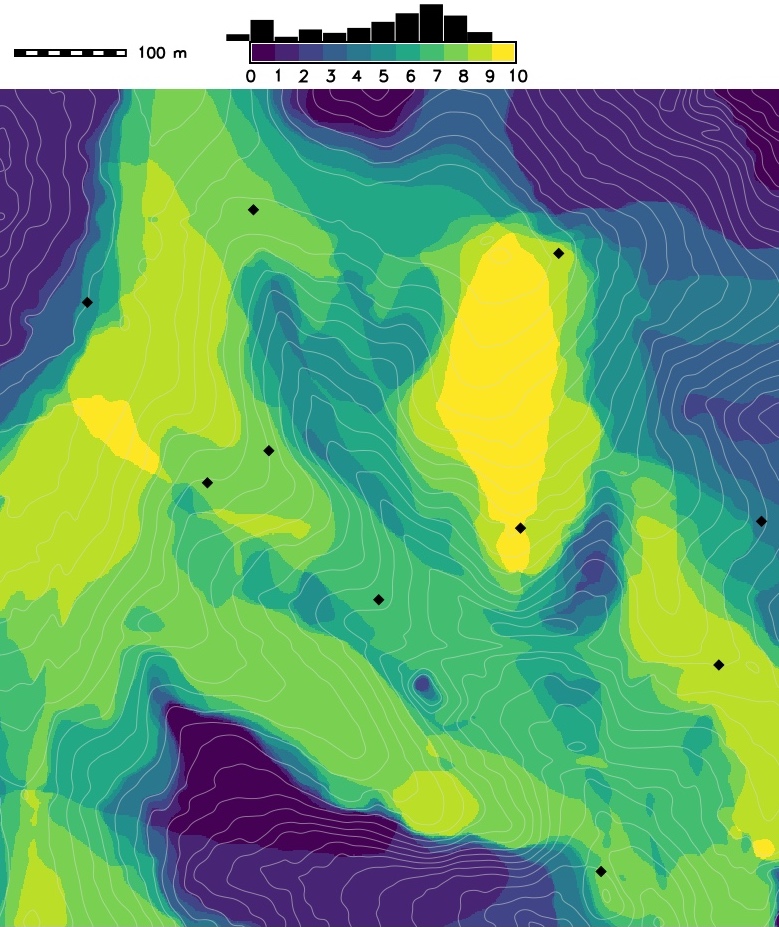
Random points

Impact of positional error on viewshed assessment: given viewing points and map showing number of points from which an area is visible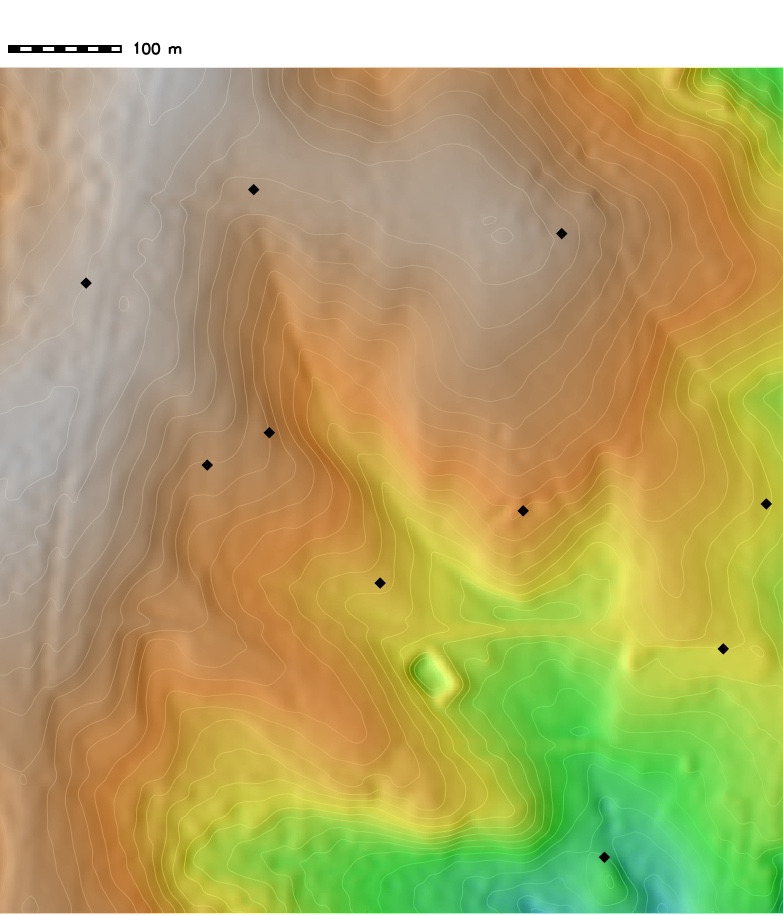

 

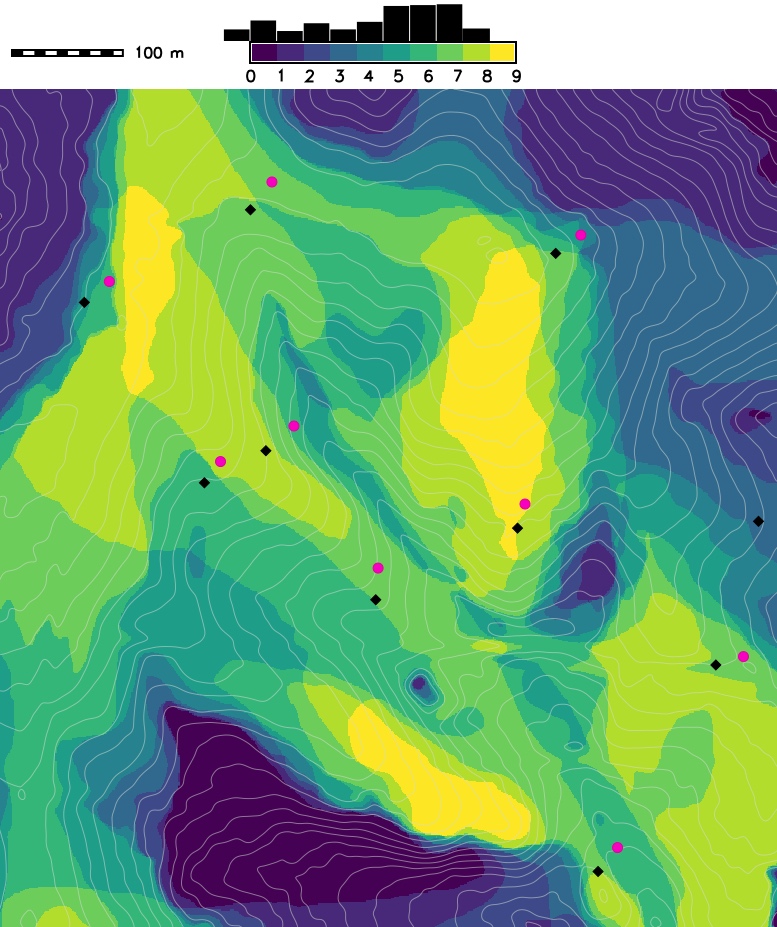
Random points with perturbation

New set of viewing points (red square) after uniform random perturbation ($d=20m$) and the resulting visibility map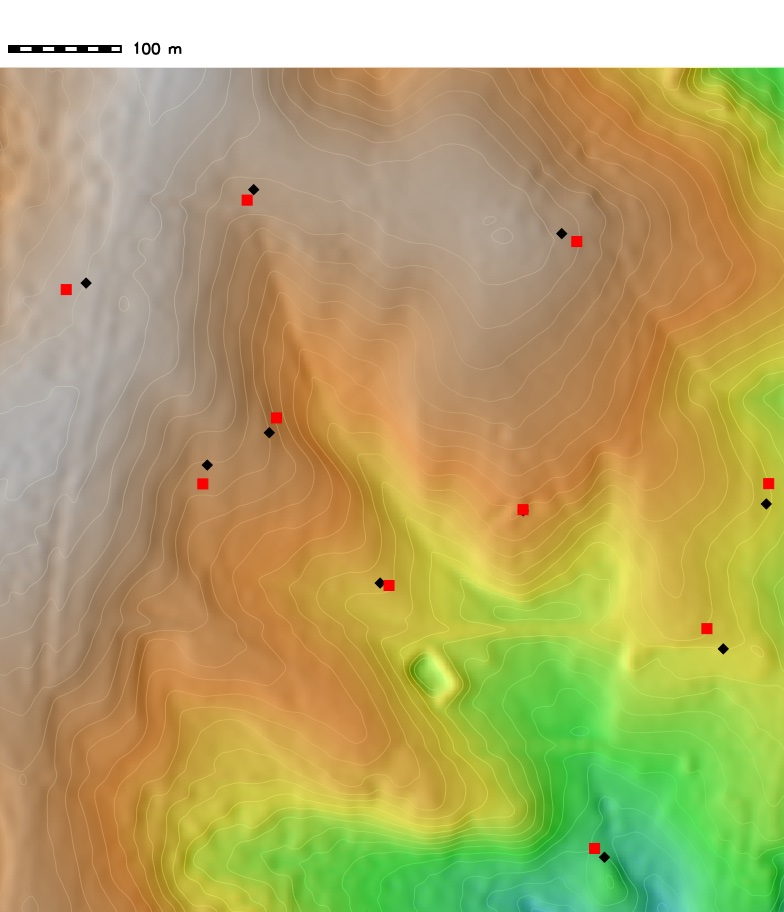

 

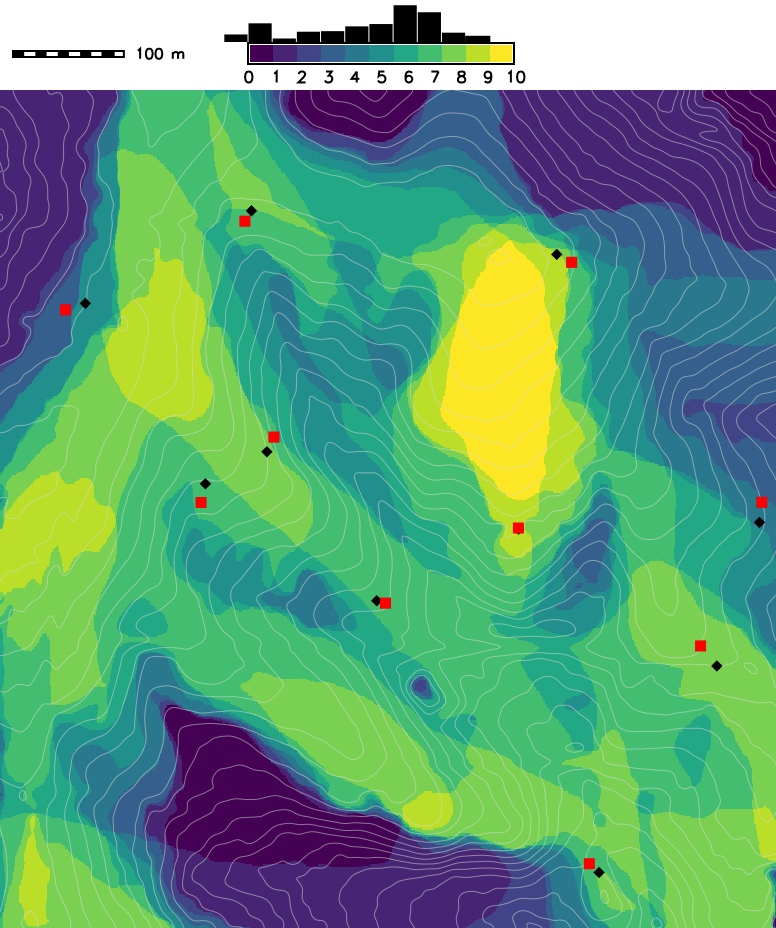
Random points with perturbation

Viewing points after perturbation with normal distribution ($\mu = 0m$, $\sigma = 15m$) and the visibility map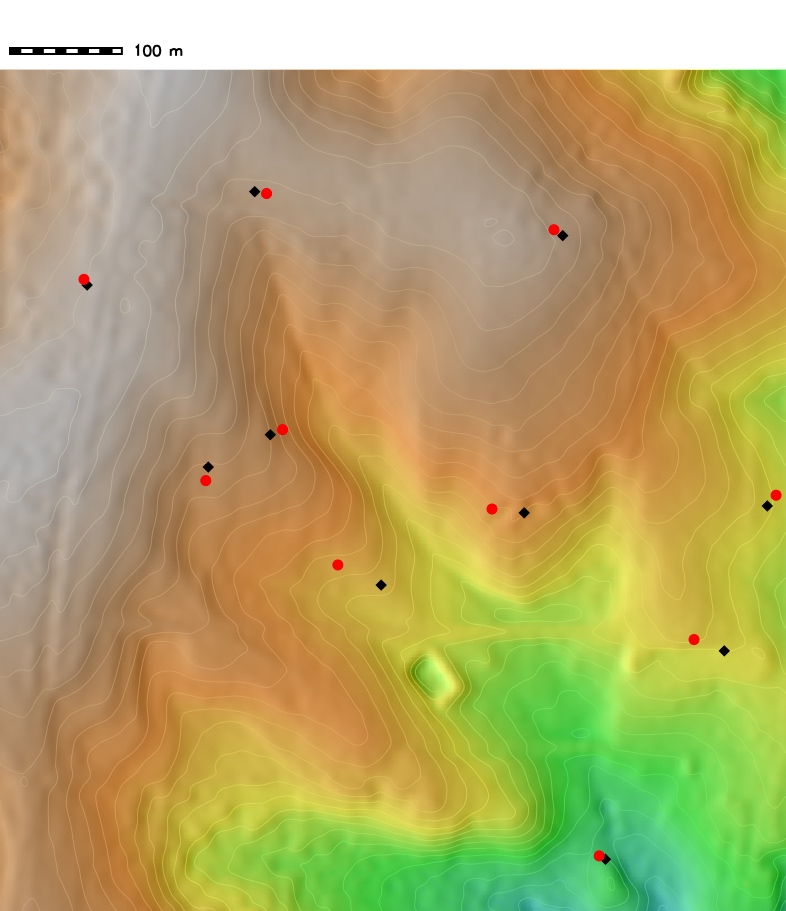

 

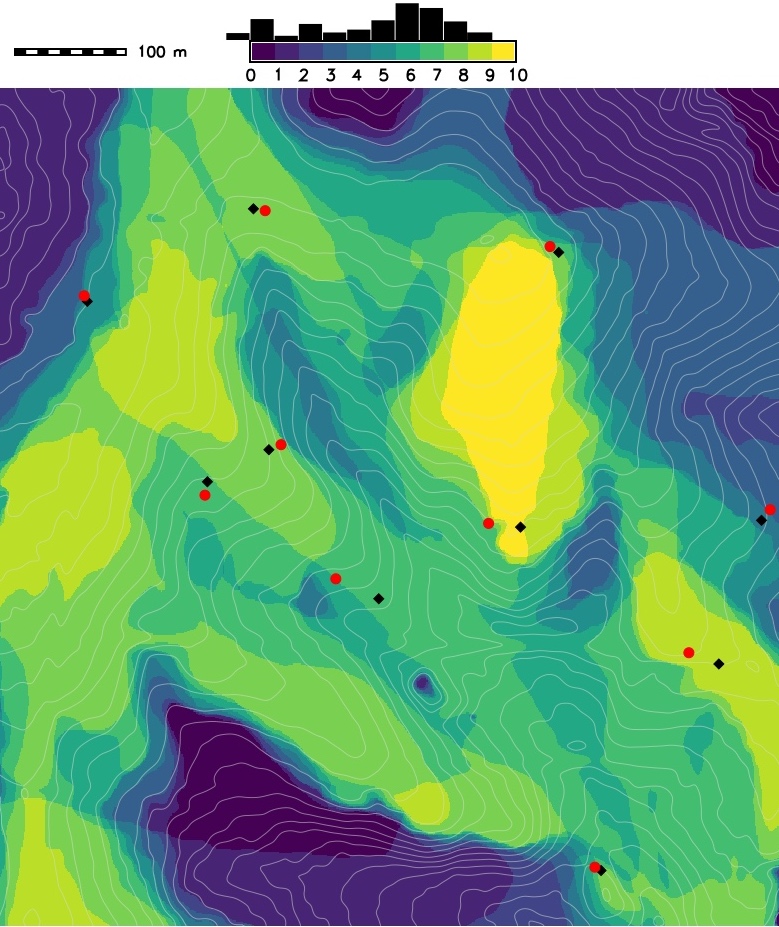
Random points with perturbation

Viewing points after perturbation with normal distribution ($\mu = 20m$, $\sigma = 7m$) simulating combined systematic and random error

 

Random points with perturbation

Random patch generators

Generating synthetic land cover / land use mapso

Summary

  • we discussed when we need data simulation
  • we defined deterministic, random, and fractal surfaces
  • we have added different type of noise to DEM and shown its impact on flow patterns
  • we explained simulation of point data and patches and their application
⌂